Commutative Algebra 37

Posted on April 25, 2020 by limsup

Artinian Modules

Instead of the ascending chain condition, we can take its reverse.

Definition.

Let M be an A-module. Consider the set $\Sigma$ of submodules of M, ordered by inclusion, i.e. $N \le N'$ if and only if $N\subseteq N'$ . We say M is artinian if $\Sigma$ is noetherian.

The ring A is said to be artinian if it is artinian as a module over itself.

Again M is artinian if either of the following equivalent conditions holds.

Every non-empty collection of submodules of M has a minimal element.
If $N_0 \supseteq N_1 \supseteq N_2 \supseteq \ldots$ is a sequence of submodules of M, then $N_k = N_{k+1} = \ldots$ for some $k\ge 0$ .

Examples

Let $A = \mathbb Z$ . This is a noetherian ring as we saw; it is not artinian because we have a decreasing sequence of ideals $(2) \supset (4) \supset (8) \supset \ldots$ .

Let $M = B / \mathbb Z$ as a $\mathbb Z$ -module where $B = \{\frac a {2^k} \in \mathbb Q : a, k \in \mathbb Z\}$ . Then M is artinian but not noetherian (exercise). We thus see that an artinian module is not finitely generated in general.

Exercise A

1. Prove that in an exact sequence of A-modules:

$0 \longrightarrow N \longrightarrow M \longrightarrow P \longrightarrow 0$ ,

M is artinian if and only if N and P are. In particular, the direct sum of two artinian modules is artinian.

2. Prove that if M is a noetherian A-module, any surjective linear $f:M\to M$ is also injective. State and prove the dual statement for an artinian module.

Decide if each of the following statements is true.

3. The product of any two artinian rings is artinian.

4. Any quotient of an artinian ring is artinian.

5. Any localization of an artinian ring is artinian.

blue-lin

Simple Modules

Let A be a fixed ring throughout this article and M be an A-module.

Definition.

M is said to be simple if it is non-zero and has no submodules except 0 and itself.

We immediately have the following.

Lemma 1.

M is simple if and only if $M \cong A/\mathfrak m$ for some maximal ideal $\mathfrak m \subset M$ .

Proof

(⇒) Pick a non-zero $m\in M$ and consider the A-linear map $f:A\to M$ , $a \mapsto am$ . Its image is a non-zero submodule of M so it is the whole M; hence f is surjective. We have $A / \mathrm{ker} f \cong M$ and submodules of M correspond to ideals of A containing ker f. Thus ker f is maximal.

(⇐) Submodules of $A/\mathfrak m$ correspond to ideals of A containing $\mathfrak m$ . Thus M is simple ⟹ $\mathfrak m$ is maximal. ♦

Example

Thus we see that simple modules over a coordinate ring k[V] (k algebraically closed) correspond to points on V. Even though we have $A/\mathfrak m_P \cong k$ as k-algebras, different points correspond to different A-modules!

Easy Exercise

Prove that for any ideals $\mathfrak a, \mathfrak b$ of A, $A / \mathfrak a \cong A/\mathfrak b$ as A-modules if and only if $\mathfrak a= \mathfrak b$ .

blue-lin

Composition Series

Next we would like to “factor” a module into its constituents comprising of simple modules.

Definition.

A composition series for M is a sequence of submodules

$0 = M_0 \subsetneq M_1 \subsetneq M_2 \subsetneq \ldots \subsetneq M_n = M$

such that $M_{i+1}/M_i$ is simple for all $i=0, \ldots, n-1$ . The length of the composition series is n; the composition factors of the series are the isomorphism classes of $M_{i+1}/M_i$ , treated as a multi-set.

Example

Let $V = \mathbb A^2(\mathbb C)$ and $W_1, W_2 \subset V$ be varieties cut out by the equations $f = Y - X^3 + 3X$ and $g = Y - 2$ respectively.

intersection_example_again

Recall that their scheme intersection (exercise D here) has coordinate ring

$\begin{aligned} A := k[W_1] \otimes_{k[V]} k[W_2] &\cong k[X, Y]/(Y - X^3 + 3X, Y - 2)\\ &\cong k[X]/(X^3 - 3X - 2)\\ &\cong k[X] / (X+1)^2 \times k[X] / (X-2) \end{aligned}$

by Chinese Remainder Theorem. In fact, the above are all isomorphisms as algebras over $k[V] = k[X, Y]$ where we have identified $k[X]$ with $k[X, Y]/(Y)$ . Thus we have the following composition series

$0 \subset (X+1)^2 A \subset (X+1) A \subset A.$

This has length 3; the composition factors are two copies of $A/(X+1)$ and one copy of $A/(X-2)$ .

Proposition 1.

M has a composition series if and only if it is a noetherian and artinian module.

Proof

(⇒) Suppose $0 = M_0 \subsetneq M_1 \subsetneq \ldots \subsetneq M_n = M$ is a composition series. Each $M_{i+1}/M_i$ is simple hence both artinian and noetherian. By induction one shows that all $M_i$ are noetherian and artinian.

(⇐) Conversely suppose M is both noetherian and artinian; we may assume $M\ne 0$ . If M has no simple submodule, we can find an infinitely decreasing sequence of submodules $M_1 \supsetneq M_2 \supsetneq \ldots$ , contradicting the fact that M is artinian. Hence we pick any simple submodule $M_1 \subseteq M$ . If $M = M_1$ we are done; otherwise, we repeat the process with $M/M_1$ and obtain a simple submodule $M_2/M_1 \subseteq M/M_1$ . This gives the next term for a composition series $0\subsetneq M_1 \subsetneq M_2 \subseteq M$ , etc. Since M is noetherian, the process must eventually terminate. ♦

Corollary 1.

If M has a composition series, so do any submodule and quotient module of M.

blue-lin

Uniqueness of Composition Series

Theorem 1.

Let M be a noetherian and artinian A-module. The composition factors of any composition series are unique up to isomorphism and reordering.

Note

For a composition series $M_0 \subset M_1 \subset \ldots \subset M_n$ we write $\mathrm{CF}(M_0, \ldots, M_n)$ for the multi-set of its composition factors.

Proof

The proof is by contradiction; say a module is bad if it has two composition series with different sets of composition factors.

Step 1: Assume M is minimal.

Take the collection Σ of all bad submodules of M. Since M is artinian, we can replace M by a minimal element of Σ. Thus M has two composition series

$0 = M_0 \subset M_1 \subset \ldots \subset M_m = M, \quad 0 = N_0 \subset N_1 \subset \ldots \subset N_n = M$

such that $\mathrm{CF}(M_0, \ldots, M_m) \ne \mathrm{CF}(N_0, \ldots, N_n)$ ; and no other submodule of M has this property.

Step 2: Consider the easy case.

Clearly $M\ne 0$ so $m,n \ge 1$ . If $M_{m-1} = N_{n-1}$ then by minimality this is a good module so $M_0 \subset \ldots \subset M_m$ and $N_0 \subset \ldots \subset N_n$ have the same composition factors, a contradiction.

Step 3: Do the “diamond argument”.

Otherwise we have $M_{m-1} + N_{n-1} = M$ which gives us

$M / M_{m-1} = (M_{m-1} + N_{n-1})/M_{m-1} \cong N_{n-1} / (M_{m-1} \cap N_{n-1})$

and similarly $M / N_{n-1} \cong M_{m-1} / (M_{m-1} \cap N_{n-1})$ .

Step 4: Apply induction.

Pick any composition series $0 = P_0 \subset \ldots \subset P_k = M_{m-1} \cap N_{n-1}$ for $M_{m-1} \cap N_{n-1}$ . Using (P) to denote the isomorphism class of a module P we have:

$\begin{aligned} \mathrm{CF}(M_0, \ldots, M_m) &= (M/M_{m-1}) + \mathrm {CF}(M_0, \ldots, M_{m-1}) \\ &= (M/M_{m-1}) + (M_{m-1} / (M_{m-1} \cap N_{n-1})) + \mathrm{CF}(P_0, \ldots, P_k) \\ &= (M/N_{n-1}) + (N_{n-1} / (M_{m-1} \cap N_{n-1})) + \mathrm{CF}(P_0, \ldots, P_k)\\ &= (M/N_{n-1}) + \mathrm{CF}(N_0, \ldots, N_{n-1}) \\ &= \mathrm{CF}(N_0, \ldots, N_n).\end{aligned}$

The second and fourth equalities follow from the fact that $M_{m-1}$ and $N_{n-1}$ are not bad, since M is a minimal bad module. The third equality follows from step 3. In diagram form we have the following.

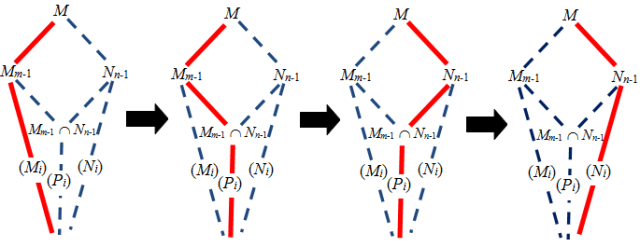
This completes our proof. ♦

Corollary 2.

If M is a noetherian and artinian module, write $l(M)$ (length of M) for the length of any composition series of M. This is a well-defined value.

Similarly, we can define the composition factors of M and denote it by $\mathrm{CF}(M)$ .

Note that if $0 \to N \to M \to P \to 0$ is an exact sequence of A-modules and M has finite length, then

$l(M) = l(N) + l(P), \quad \mathrm{CF}(M) = \mathrm{CF}(N) + \mathrm{CF}(P).$

This gives another application of short exact sequences.

Exercise B

1. Compute the length and composition series of

$B = \mathbb R[X]/ (X^6 + X^2)$

as an B-module.

2. Prove that for a ring quotient $B = A/\mathfrak a$ , a B-module M is noetherian (resp. artinian) as a B-module if and only if it is so as an A-module.

In the next article, we will look at artinian rings. It turns out this is a small subclass of the collection of noetherian rings.

Optional Note

All the results in this section can be generalized to left modules over a non-commutative ring. This has applications in representation theory, since a simple module over the group algebra $k[G]$ (k = any field) corresponds to an irreducible k-representation of G.

blue-lin

Posted in Advanced Algebra | Tagged artinian, composition factors, composition series, length of module, noetherian, simple modules | Leave a comment

Commutative Algebra 36

Posted on April 24, 2020 by limsup

In this article, we will study the topology of Spec A when A is noetherian. For starters, let us consider irreducible topological spaces in greater detail.

Irreducible Spaces

Recall that an irreducible topological space is a non-empty space X satisfying any of the three equivalent conditions.

Any non-empty open subset of X is dense.
If $U, V\subseteq X$ are non-empty open subsets then $U\cap V\ne\emptyset$ .
If $C, D\subseteq X$ are closed subsets whose union is X, then C = X or D = X.

Now let us go through some basic properties of irreducible topological spaces.

Proposition 1.

A non-empty open subset U of an irreducible space X is irreducible.

Proof

Let $V, W\subseteq U$ be non-empty open subsets. Then they are non-empty open subsets of X also, so $V\cap W \ne\emptyset$ . ♦

Proposition 2.

Let $Y\subseteq X$ be a non-empty dense subset of X. If Y is irreducible so is X.

In other words, the closure of an irreducible subspace is irreducible.

Proof

For any subset A of a topological space X we let $\mathrm{cl}_X(A)$ be the closure of A in X. We will use the topological fact: if $A\subseteq Y \subseteq X$ then $\mathrm{cl}_Y(A) = \mathrm{cl}_X(A) \cap Y$ .

Let $U\subseteq X$ be a non-empty open subset. Since Y is dense in X, $V := U\cap Y$ is a non-empty open subset of Y. We have $\mathrm{cl}_Y(V) = \mathrm{cl}_X(V) \cap Y$ , but since Y is irreducible $\mathrm{cl}_Y(V) = Y$ . Hence $\mathrm{cl}_X(V) \supseteq Y$ . Since Y is dense in X we have $\mathrm{cl}_X(V) = X$ . ♦

Exercise A

Decide if this statement is true: let $Y\subseteq X$ be a non-empty dense subset of X. If X is irreducible, so is Y.

Proposition 3.

Let $f:X\to Y$ be a continuous map. If X is irreducible, so is $f(X)$ .

Proof

Let $U, V\subseteq f(X)$ be non-empty open subsets. Then $f^{-1}(U), f^{-1}(V)$ are non-empty open subsets of X so $f^{-1}(U\cap V) = f^{-1}(U) \cap f^{-1}(V) \ne \emptyset$ . Thus $U\cap V \ne\emptyset$ . ♦

Proposition 4.

If X, Y are irreducible topological spaces, so is $X\times Y$ .

Proof

Pick two non-empty open subsets of $X\times Y$ ; we wish to prove they intersect.

The open sets of the type $U\times V$ ( $U\subseteq X, V\subseteq Y$ open) form a basis of $X\times Y$ . Hence, we may assume the two open sets we picked were $U_1 \times V_1$ and $U_2 \times V_2$ , where $U_1, U_2 \subseteq X$ and $V_1, V_2\subseteq Y$ are open. Since these are all non-empty,

$U_1 \cap U_2 \ne \emptyset, V_1 \cap V_2 \ne \emptyset \implies (U_1 \times V_1) \cap (U_2 \times V_2) \ne\emptyset$ . ♦

Exercise B

Let k be an algebraically closed field. Prove that if V and W are irreducible affine k-varieties so is their product $V\times W$ . [ Warning: this is not the product topology, as we noted earlier. ]

Prove that if A and B are finitely generated k-algebras which are integral domains, so is $A\otimes_k B$ . Find a counter-example when k is not algebraically closed.

blue-lin

Noetherian Topological Spaces

Following the idea of considering Spec A as the set of prime ideals of A, with closed sets corresponding to ideals, we define:

Definition.

A topological space is said to be noetherian if its collection of closed subsets forms a noetherian poset, when they are ordered by inclusion.

In other words, X is noetherian if and only if the following equivalent conditions hold.

Any non-empty collection of closed subsets of X has a minimal element.
If $Y_1 \supseteq Y_2 \supseteq \ldots$ is a sequence of closed subsets of X then for some n we have $Y_n = Y_{n+1} = \ldots$ .

Since the closed subsets of Spec A correspond bijectively to radical ideals, we have:

Proposition 5.

The spectrum of a noetherian ring is noetherian.

warning It is possible for a non-noetherian ring to have a noetherian spectrum. For example if $A = k[X_1, X_2, \ldots ]/(X_1^2, X_2^2, \ldots)$ then A has exactly one prime ideal but it is not noetherian.

Exercise C

Decide if each of the following claims is true.

A subspace of a noetherian topological space is noetherian.
A product of two noetherian topological spaces is noetherian.
If $Y_1, Y_2 \subseteq X$ are noetherian subspaces, then so is $Y_1 \cup Y_2$ .
If $f:X\to Y$ is continuous and X is noetherian, then so is $f(X)$ .

blue-lin

Irreducible Components

Definition.

An irreducible component of X is a non-empty maximal irreducible subset $C\subseteq X$ .

We get the following.

Proposition 6.

Every non-empty irreducible subset $Y\subseteq X$ is contained in an irreducible component.

Note

Since the closure of an irreducible set in a space is irreducible, any irreducible component of X is closed in X.

Proof

Let $\Sigma$ be the collection of all irreducible subsets of X containing Y, ordered by inclusion. Note that $Y\in\Sigma$ so $\Sigma \ne \emptyset$ . It suffices to apply Zorn’s lemma to this set, so we need to show that any chain $\Sigma'\subseteq \Sigma$ has an upper bound. Hence it suffices to show $C := \cup_{Z\in \Sigma'} Z$ is irreducible.

Suppose $U, V \subseteq C$ are disjoint non-empty open subsets. Then $U\cap Z_1 \ne \emptyset$ and $V\cap Z_2 \ne\emptyset$ for some $Z_1, Z_2 \in \Sigma'$ . Since $\Sigma'$ is a chain we may assume without loss of generality that $Z_1 \subseteq Z_2$ . This gives $U \cap Z_2, V \cap Z_2\ne\emptyset$ , non-empty disjoint open subsets of $Z_2$ , which contradicts irreducibility of $Z_2$ . ♦

Easy Exercise

Find the irreducible components of $\mathbb R$ under (i) the usual topology, (ii) the cofinite topology (where the only closed subsets are the finite subsets and $\mathbb R$ itself).

blue-lin

Components of Noetherian Space

Lemma 1.

Let $C_1, \ldots, C_k \subseteq X$ be irreducible components of X. If $Y \subseteq C_1 \cup \ldots \cup C_k$ is irreducible then $Y\subseteq C_i$ for some i.

Proof

Apply induction on k; when k = 1 there is nothing to prove so assume k > 1. Since irreducible components are closed, Y is the union of closed subsets

$D := Y \cap C_k, \quad D' := Y \cap (C_1 \cup \ldots \cup C_{k-1})$

so by irreducibility of Y we have Y = D or Y = D’. In the former case we are done since $Y \subseteq C_k$ . In the latter case $Y \subseteq C_1 \cup \ldots \cup C_{k-1}$ so by induction hypothesis $Y \subseteq C_i$ for some $1\le i \le k-1$ . ♦

Proposition 7.

A noetherian space X has only finitely many irreducible components $C_1, \ldots, C_k$ . Furthermore, for any $1\le i \le k$ we have

$C_i \not\subseteq \cup_{j\ne i} C_j.$

Proof

The second statement follows from lemma 1. For the first statement, let $\Sigma$ be the collection of all closed subsets of X which are not finite unions of irreducible subsets. It suffices to show $\Sigma$ is empty.

If not $\Sigma$ has a minimal element C; since C is not irreducible we can write $C = C_1 \cup C_2$ where $C_1, C_2 \subsetneq C$ are closed subsets of C. Since $C\in\Sigma$ is minimal we have $C_1, C_2 \not\in\Sigma$ . Thus each of them is a finite union of irreducible subsets, and so is C, a contradiction. ♦

blue-lin

Geometric Interpretation

Let us interpret the above for X = Spec A. Recall (proposition 6 here) that the irreducible closed subsets of X correspond to prime ideals of A. Thus the irreducible components correspond to minimal primes of A and we have again shown that every prime ideal of A contains a minimal prime. Since a noetherian space has only finitely many irreducible components we have:

Proposition 8.

A noetherian ring has only finitely many minimal primes.

Example

Let $V\subset \mathbb A^3(\mathbb C)$ be the variety defined by the equations

$f(X, Y, Z) = X^2 - YZ, \quad g(X, Y, Z) = X^3 - Y.$

Solving gives us $XYZ = Y$ and hence $Y=0$ or $XZ=1$ . The first case gives the z-axis $X=Y=0$ while the second case gives a hyperbola $(X, Y, Z) = (X, X^3, \frac 1 X)$ for $X\in \mathbb C - \{0\}$ . Hence V has two irreducible components. The corresponding minimal primes of $A = \mathbb C[X, Y, Z]/(X^2 - YZ, X^3 - Y)$ are:

$\mathfrak p_1 = (X, Y), \quad \mathfrak p_2 = (XZ - 1, Y - X^3).$

To compute the nilradical of A, use the following facts (proof: exercise).

The nilradical of a ring quotient $B/\mathfrak b$ is exactly $r(\mathfrak b)/\mathfrak b$ .
In a UFD B, for $b\in B$ with prime factorization $b = \prod_{i=1}^r \pi_i^{e_i}$ , the radical of the principal ideal (b) is $(\prod_{i=1}^r \pi_i)$ .

Now A is isomorphic to $\mathbb C[X, Z]/(X^2 - X^3 Z)$ . Since $\mathbb C[X, Z]$ is a UFD, the radical of A is $(X(1-XZ))/(X^2 - X^3 Z)$ . Hence the intersection of all prime ideals of A is $(X(1-XZ))$ so

$\mathfrak p_1 \cap \mathfrak p_2 = (X(1-XZ)).$

blue-lin

Posted in Advanced Algebra | Tagged irreducible components, irreducible spaces, noetherian, noetherian spaces, zariski topology | Leave a comment

Commutative Algebra 35

Posted on April 23, 2020 by limsup

Noetherian Modules

Through this article, A is a fixed ring. For the first two sections, all modules are over A.

Recall that a submodule of a finitely generated module is not finitely generated in general. This will not happen if we constrain ourselves to a better behaved class of modules.

Definition.

Let M be an A-module. Consider the set $\Sigma$ of submodules of M, ordered by reverse inclusion, i.e. $N \le N'$ if and only if $N'\subseteq N$ . We say M is noetherian if $\Sigma$ is a noetherian poset.

By proposition 1 here, M is noetherian if either of the following equivalent conditions holds.

Every non-empty collection of submodules of M has a maximal element.
If $N_0 \subseteq N_1 \subseteq N_2 \subseteq \ldots$ is a sequence of submodules of M, then $N_k = N_{k+1} = \ldots$ for some $k\ge 0$ .

Philosophically, noetherian is a type of “finiteness” condition on modules as the results below show.

Proposition 1.

Given an exact sequence of A-modules:

$0 \longrightarrow N \longrightarrow M \longrightarrow P \longrightarrow 0$ ,

M is noetherian if and only if N and P are.

Proof

Without loss of generality, we assume $N\subseteq M$ and $P = M/N$ .

(⇒) Suppose M is noetherian. N is noetherian since submodules of N are submodules of M. Similarly, P is noetherian since submodules of P correspond bijectively to submodules of M containing N.

(⇐) Let $M_0 \subseteq M_1 \subseteq \ldots$ be a sequence of submodules of M. We get sequences of submodules

$M_0 \cap N \subseteq M_1 \cap N \subseteq \ldots \subseteq N, \quad (M_0 + N)/N \subseteq (M_1 + N)/N \subseteq \ldots \subseteq M/N.$

Since N and M/N are noetherian, there is a k such that $M_k \cap N = M_{k+1} \cap N = \ldots$ and $M_k + N = M_{k+1} + N = \ldots$ . Now apply the following to finish to job. ♦

Exercise A

Prove that if $Q \subseteq Q'$ and N are submodules of M such that $Q\cap N = Q'\cap N$ and $Q+N = Q'+N$ , then $Q = Q'$ .

Corollary 1.

If M and N are noetherian modules, so is $M\oplus N$ .

If N and N’ are noetherian submodules of M, so is N + N’ (because it is a quotient of $N\oplus N'$ ).

blue-lin

Classification of Noetherian Modules

Lemma 1.

A noetherian module M is finitely generated.

Proof

Take the set of all finitely generated submodules of M. Since M is noetherian it has a maximal element $M_0$ . If $M_0 \ne M$ pick any $x\in M - M_0$ . Then $M_0 + (x)$ is a finitely generated submodule of M which properly contains $M_0$ , which contradicts maximality of $M_0$ . ♦

Proposition 2.

A module M is noetherian if and only if every submodule is finitely generated.

Proof

(⇒) Any submodule of a noetherian module is noetherian, and hence finitely generated.

(⇐) Pick any sequence of submodules $N_0 \subseteq N_1 \subseteq \ldots$ of M. Let $N = \cup_i N_i$ . Show that this is a submodule of M. By the given condition it is finitely generated by, say, $x_1, \ldots, x_k$ . Then for some n we have $x_1, \ldots, x_k \in N_n$ . It follows that $N_n = N_{n+1} = \ldots = N$ . ♦

Definition.

The ring A is noetherian if it is noetherian as a module over itself. By proposition 2, A is noetherian if and only if all its ideals are finitely generated.

In particular, a noetherian ring A satisfies a.c.c. on the set of its principal ideals. Hence in a noetherian integral domain, every non-zero element $a\in A$ can be factored as a product of irreducibles.

Proposition 3.

If the ring A is noetherian, an A-module M is noetherian if and only if it is finitely generated.

Proof

(⇒) Apply lemma 1. (⇐) Since A is noetherian as an A-module, so is any finite direct sum $A^n$ . And since $M$ is finitely generated, it is a quotient of some $A^n$ ; hence M is noetherian. ♦

In summary, the class of finitely generated modules over noetherian rings is well-behaved: it is closed under taking submodules, quotient modules, finite direct sums and finite sums of submodules.

Exercise B

Let M, N be modules; prove the following.

If M and N are finitely generated, so is $M\otimes_A N$ .
If M is noetherian and N is finitely generated, then $M\otimes_A N$ is noetherian.

blue-lin

Constructing Noetherian Rings

Thus the question now stands: which rings are noetherian? Obviously fields are noetherian, having only two ideals. Next we have the following easy constructions.

Lemma 2.

Any principal ideal domain is noetherian.

Proof

Indeed we showed earlier that A satisfies a.c.c. on principal ideals. But all ideals of A are principal. ♦

Lemma 3.

If A is a noetherian ring, so is any localization $S^{-1}A$ .

Proof

We showed that any ideal of $S^{-1}A$ is of the form $\mathfrak a (S^{-1}A)$ for some ideal $\mathfrak a \subseteq A$ . If $\mathfrak a$ is generated by $x_1, \ldots, x_n$ then $\mathfrak a(S^{-1}A)$ is generated by $\frac {x_1} 1, \ldots, \frac{x_n}1$ . ♦

Lemma 4.

If A and B are noetherian rings, so is $A\times B$ .

Proof

We saw that any ideal of $A\times B$ is of the form $\mathfrak a \times \mathfrak b$ where $\mathfrak a, \mathfrak b$ are ideals of A, B respectively. ♦

Lemma 5.

If A is noetherian, so is any quotient $A/\mathfrak a$ .

Proof

Any ideal of $A/\mathfrak a$ is of the form $\mathfrak b/\mathfrak a$ where $\mathfrak b \subseteq A$ is an ideal, so it is finitely generated. ♦

blue-lin

Hilbert Basis Theorem

Hilbert Basis Theorem.

If A is a noetherian ring, so is $A[X]$ .

Proof

Suppose $\mathfrak b \subseteq A[X]$ is not finitely generated; we pick $f_0 \in \mathfrak b - \{0\}$ of minimum degree. Recursively, pick $f_n \in \mathfrak b - (f_0, f_1, \ldots, f_{n-1})$ of minimum degree. Let $d_i = \deg f_i$ so that $d_0 \le d_1 \le \ldots$ . Suppose the leading term of $f_i$ is $a_i X^{d_i}$ , where $a_i \in A$ .

The sequence $(a_0) \subseteq (a_0, a_1) \subseteq \ldots$ of ideals of A eventually terminates so $a_n \in (a_0, a_1, \ldots, a_{n-1})$ for some n. We write $a_n = r_0 a_0 + \ldots + r_{n-1} a_{n-1}$ for some $r_0, \ldots, r_{n-1} \in A$ . Now

$\begin{aligned} r_0 X^{d_n - d_0} f_0 &= r_0 a_0 X^{d_n} + (\text{smaller terms}), \\ r_1 X^{d_n - d_1} f_1 &= r_1 a_1 X^{d_n} + (\text{smaller terms}), \\ &\vdots \\ r_{n-1} X^{d_n - d_{n-1}} f_{n-1} &= r_{n-1} a_{n-1} X^{d_n} + (\text{smaller terms}).\end{aligned}$

Let g be the sum of all these polynomials; then $g\in \mathfrak b$ has degree $d_n$ and leading coefficient $\sum_{i=0}^{n-1} r_i a_i = a_n$ . Hence $f_n - g \in \mathfrak b$ has degree $< d_n$ and lies outside $(f_0, \ldots, f_{n-1})$ , which contradicts minimality of $\deg f_n$ . ♦

Immediately we have:

Corollary 2.

If A is a noetherian ring, so is any finitely generated A-algebra.

Proof

Such an algebra must be a (ring) quotient of $A[X_1, \ldots, X_n]$ for some n. ♦

Examples

Any finitely generated algebra over a field or $\mathbb Z$ is noetherian; more generally any localization of such a ring is noetherian.

Exercise C

Prove the following for A-algebras B and C.

If B and C are of finite type over A, so is $B\otimes_A C$ .
If B is of finite type over A, and C is noetherian, then $B\otimes_A C$ is noetherian.

Note

In most cases of interest (e.g. algebraic number theory and algebraic geometry), our rings and modules will be noetherian.

warning Most A-algebras we look at are of finite type over A but not finite over A. In other words, they are finitely generated as A-algebras but not as A-modules. Thus, if we look at such an algebra as an A-module, it is no longer noetherian and we have to be careful in applying the above results.

Next, by proposition 1 here, if M is a finitely generated module over a noetherian ring, it is flat if and only if it is projective. But that does not mean we can safely ignore their difference when dealing with concrete examples, for in the case of flatness, we are usually more interested in flat algebras rather than modules.

In summary:

flat A-algebras correspond to families of varieties which “vary nicely”;
projective A-modules correspond to locally free vector bundles.

blue-lin

Posted in Advanced Algebra | Tagged flat modules, hilbert basis theorem, ideals, modules, noetherian, projective modules | Leave a comment

Commutative Algebra 34

Posted on April 22, 2020 by limsup

Nakayama’s Lemma

The following is a short statement which has far-reaching applications. Since its main applications are for local rings, we will state the result in this context. Throughout this section, $(A, \mathfrak m)$ is a fixed local ring.

Theorem (Nakayama’s Lemma).

Let M be a finitely generated A-module. Then

$\mathfrak m M = M \implies M = 0$ .

In other words, if $M\ne 0$ then $k(\mathfrak m) \otimes M \cong M/\mathfrak m M \ne 0$ , where $k(\mathfrak m)$ is the residue field.

Proof (Lang)

Suppose $m_1, \ldots, m_n \in M$ is a minimal set of generators of M. If n = 0, M = 0 and we are done. Otherwise, we have $m_1 \in M = \mathfrak m M$ so we can write

$m_1 = a_1 m_1 + \ldots + a_n m_n, \quad a_1, \ldots, a_n \in \mathfrak m.$

But since $a_1 \in \mathfrak m$ , we have $1-a_1 \in A$ a unit, so in fact:

$m_1 = (1 - a_1)^{-1} (a_2 m_2 + \ldots + a_n m_n)$

and M has a smaller set of generators given by $m_2, \ldots, m_n$ (contradiction). ♦

Corollary 1.

Let M be a finitely generated module over $(A, \mathfrak m)$ and $m_1, \ldots, m_n \in M$ . If $\overline m_1, \ldots, \overline m_n \in M/\mathfrak m M$ span it as a vector space over $A/\mathfrak m$ , then $m_1, \ldots, m_n \in M$ generate it as an A-module.

Proof

Let $f:A^n \to M$ be the A-linear map which takes $e_i \mapsto m_i$ . Let C be the cokernel of f so we get an exact sequence of A-modules: $A^n \stackrel f \to M \to C \to 0$ . Since the functor $N \mapsto N/\mathfrak m N$ is right-exact (by corollary 2 here), we get an exact:

$(A/\mathfrak m)^n \stackrel{\overline f}\longrightarrow M/\mathfrak m M \longrightarrow C/\mathfrak m C \longrightarrow 0$

By the given condition $\overline f$ is surjective so $C = \mathfrak m C$ . Since C is finitely generated (being a quotient of M), we have C = 0. ♦

Hence, for a finitely generated M over $(A, \mathfrak m)$ , let $n = \dim_{A/\mathfrak m} M/\mathfrak m M$ and pick $m_1, \ldots, m_n$ such that $\overline m_i \in M/\mathfrak m M$ form a basis over $A/\mathfrak m$ . Then $m_1, \ldots, m_n$ form a minimal generating set for M over A. Furthermore, all minimal generating sets of M have the same cardinality: n.

Exercise A

Prove that if $\{m_1, \ldots, m_n\}$ and $\{m_1', \ldots, m_n'\}$ are minimal generating sets of M, then

$\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{pmatrix} \begin{pmatrix} m_1 \\ m_2 \\ \vdots \\ m_n\end{pmatrix} = \begin{pmatrix} m_1 \\ m_2 \\ \vdots \\m_n\end{pmatrix}$

for some invertible matrix $(a_{ij})$ with entries in A.

blue-lin

Cotangent Spaces

Again $(A, \mathfrak m)$ denotes a local ring. Inspired by our earlier computation of tangent spaces, we define:

Definition.

The cotangent space of A is given by $\mathfrak m / \mathfrak m^2$ . More generally, for $r\ge 1$ , the r-th order cotangent space of A is $\mathfrak m^r / \mathfrak m^{r+1}$ .

Exercise B

Find a local ring $(A, \mathfrak m)$ which is not a field, satisfying $\mathfrak m = \mathfrak m^2$ .

[ Hint: take the ring of all differentiable functions ℝ → ℝ and consider the maximal ideal of all functions vanishing at 0. ]

Let us assume that $\mathfrak m$ is a finitely generated module; hence so is every $\mathfrak m^r$ . The anomaly in exercise B thus does not occur. From Nakayama’s lemma, we see that a minimal generating set of $\mathfrak m^r$ is obtained from a basis of $\mathfrak m^r/ \mathfrak m^{r+1}$ over $A/\mathfrak m$ .

In the following examples, we will let A be the coordinate ring of a variety V over k (algebraically closed field). For $P\in V$ , let $\mathfrak m = \mathfrak m_P$ so that $A/\mathfrak m \cong k$ . We can apply our above reasoning to the local ring $B := A_{\mathfrak m}$ and $\mathfrak n = \mathfrak m B$ . Note that

$\mathfrak n^r /\mathfrak n^{r+1} \cong \mathfrak m^r / \mathfrak m^{r+1}$

since the RHS is already a B-module. Thus we only need to compute:

$P(r) = \dim_{k} \mathfrak m^r / \mathfrak m^{r+1}$

to find the minimum number of generators of $\mathfrak n^r$ .

Example 1

Suppose $A = k[X_1, \ldots, X_n]$ and $\mathfrak m = (X_1, \ldots, X_n)$ . Then $A / \mathfrak m = k$ and $\mathfrak m^r / \mathfrak m^{r+1}$ has k-basis given by all monomials of degree r. The number of such monomials is the number of solutions to $a_1 + \ldots + a_n = r$ in non-negative integers. By elementary combinatorics, we have

$P(r) = {r+n-1 \choose n-1},$

which is polynomial in r of degree n-1.

In the following examples, when A is a quotient of $k[X_1, \ldots, X_n]$ we will write $X_i$ instead of $\overline X_i$ for its image in A.

Example 2

Let $A = k[X, Y]/(Y^2 - X^3 + X)$ and $\mathfrak m =(X, Y)$ . Since $X = X^3 - Y^2 \in \mathfrak m^2$ in A, any monomial of degree r which contains $X$ lies in $\mathfrak m^{r+1}$ . Thus $\mathfrak m^r / \mathfrak m^{r+1}$ has basis $Y^r$ and

$P(r) = \dim_k (\mathfrak m^r / \mathfrak m^{r+1}) = 1.$

Example 3

Let $A = k[X, Y, Z]/(Z^3 - X^3 - Y^3)$ and $\mathfrak m = (X, Y, Z)$ . In $k[X, Y, Z]$ , the elements $X, Y, Z$ do not have any linear relation modulo $(X, Y, Z)^2 + (Z^3 - X^3 - Y^3) = (X, Y, Z)^2$ , hence we have $\dim_k \mathfrak m/\mathfrak m^2 = 3$ .

Similarly, in $k[X, Y, Z]$ the monomials of degree 2 have no linear relation modulo $(X, Y, Z)^3 + (Z^3 - X^3 - Y^3) = (X, Y, Z)^3$ so we have $\dim_k \mathfrak m^2 / \mathfrak m^3 = 6$ .

For $\mathfrak m^r /\mathfrak m^{r+1}$ where $r\ge 3$ , we have $Z^3 = X^3 + Y^3$ in A so a basis is given by $X^a Y^b Z^c$ where $a+b+c = r$ and $c=0,1,2$ . Thus $P(r) = 3r$ . In conclusion

$P(r) = \begin{cases} 1, \quad &\text{if } r = 0,\\ 3r, &\text{if } r\ge 1.\end{cases}$

Note

We thus see that in all three case, the function $P(r)$ can be represented by a polynomial for sufficiently large r. This is called the Hilbert polynomial of the local ring A; we shall have more to say about this later.

Question to Ponder

What can we say about the degree of the Hilbert polynomial?

blue-lin

F. P. + Flat = F. G. + Projective

Finally, here is an interesting result. Recall that saying a module is finite presented is a stronger condition than saying it is finitely generated. On the other hand, by corollary 1 here, projective modules are flat. It turns out these two pairs of properties complement each other.

Proposition 1.

An A-module M is finitely presented and flat if and only if it is finitely generated and projective.

Note

Let us keep stock of what we already know; by the above remarks f.p. ⇒ f.g. and flat ⇐ projective. By exercise A.2 here, f.p. ⇐ f.g. + projective. Thus the only remaining case is f.p. + flat ⇒ projective.

Proof

By localization, we may assume $(A, \mathfrak m)$ is local (exercise: write out the detailed argument). Hence it suffices to show the following. ♦

Proposition 2.

A finitely presented flat module M over a local ring $(A, \mathfrak m)$ is free.

Proof

Pick a minimal generating set $m_1, \ldots, m_n \in M$ over A. Take the surjective map $A^n \to M$ which maps $e_i \mapsto m_i$ and let K be the kernel of this map. Hence we get an exact sequence

$0 \longrightarrow K \stackrel \subseteq \longrightarrow A^n \longrightarrow M \longrightarrow 0.$

By the exercise after this, tensoring this exact sequence with any A-module N gives an exact sequence. In particular, we set $N = A/\mathfrak m$ to obtain:

$0 \longrightarrow K/\mathfrak m K \longrightarrow (A/\mathfrak m)^n \longrightarrow M/\mathfrak m M \longrightarrow 0.$

But since $m_i$ ‘s form a minimal generating set of M over A, $\overline m_i \in M/\mathfrak m M$ form a basis over $A/\mathfrak m$ . Thus the map $(A/\mathfrak m)^n \to M/\mathfrak m M$ is an isomorphism and we have $K = \mathfrak m K$ . By proposition 1 here, since M is finitely presented, K is finitely generated. Thus by Nakayama’s lemma K = 0 and $M \cong A^n$ . ♦

It remains to fill in the gap in the proof.

Exercise C

Suppose we have a short exact sequence of A-modules

$0 \longrightarrow M_1 \longrightarrow M_2 \longrightarrow M \longrightarrow 0$

where M is A-flat. Then tensoring with any A-module N gives a short exact sequence:

$0 \longrightarrow M_1 \otimes_A N \longrightarrow M_2 \otimes_A N \longrightarrow M \otimes_A N \longrightarrow 0.$

[ Hint: let $F\to N$ be a surjective map where F is free; let K be its kernel so we get a short exact sequence $0\to K \to F \to N \to 0$ . Since M and F are flat, we have a diagram where the rows and columns are exact. Do a diagram-chase. ]

Summary.

For a finitely presented module M, the following are equivalent.

M is projective.

M is flat.

For any maximal ideal $\mathfrak m\subset A$ , $M_{\mathfrak m}$ is free over $A_{\mathfrak m}$ .

We thus see that for such modules, projectivity is a local property and being “locally free” is equivalent to being projective.

blue-lin

Posted in Advanced Algebra | Tagged cotangent spaces, finitely presented, flat modules, local rings, locally free, nakayamas lemma, projective modules | Leave a comment

Commutative Algebra 33

Posted on April 21, 2020 by limsup

Snake Lemma

Let us introduce a useful tool for computing kernels and cokernels in a complicated diagram of modules. Although it is only marginally useful for now, it will become a major tool in homological algebra.

Snake Lemma.

Suppose we have the following diagram of A-modules and homomorphisms, where the rows are exact.

Let $K_i = \mathrm{ker} h_i$ and $C_i = \mathrm{coker} h_i$ for $i = 1, 2, 3$ . Then we get a long exact sequence:

$0 \to \mathrm{ker } f_1 \to K_1 \to K_2 \to K_3 \to C_1 \to C_2 \to C_3 \to \mathrm{coker} g_2 \to 0.$

In diagram, the long exact sequence is drawn in green:

Proof

The proof is rather tedious so we will only prove the existence of the “snake map” $K_3 \to C_1$ .

Let $m_3 \in K_3$ so that $h_3(m_3) = 0$ .
Since $f_2$ is surjective there exists $m_2 \in M_2$ , $f_2(m_2) = m_3$ .
Let $n_2 = h_2(m_2)$ .
Then $g_2(n_2) = g_2(h_2(m_2)) = h_3(f_2(m_2)) = h_3(m_3) = 0$ .
Hence $n_2 = g_1(n_1)$ for a unique $n_1 \in N_1$ .
We let $m_3 \mapsto$ image of $n_1$ in $C_1$ .

This map is well-defined since if we pick another $m_2' \in M_2$ in the second step, then $m_2' - m_2 \in \mathrm{ker} f_2 = \mathrm{im } f_1$ . Thus $m_2' - m_2 = f_1(m_1)$ for some $m_1 \in M_1$ so $h_2(m_2' - m_2) = h_2(f_1(m_1)) = g_1(h_1(m_1))$ and thus the new $n_1' \in N_1$ in the above construction is $n_1' = n_1 + h_1(m_1)$ . So $n_1$ and $n_1'$ have the same image in $\mathrm{coker} h_1$ .

The rest of the proof is left as an exercise. ♦

Note

The above process is called diagram-chasing, and it is often far more effective to have it shown to you live. Here is the first part of the proof in video form.

blue-lin

Finitely Presented Modules

Now let us compare $\mathrm{Hom}_B(M^B, N^B)$ and $\mathrm{Hom}_A(M, N)$ for A-modules M and N. Since any A-linear map $f: M\to N$ induces a B-linear map $f^B : M^B \to N^B$ we have a map $\mathrm{Hom}_A(M, N) \to \mathrm{Hom}_B(M^B, N^B)$ . This is clearly A-linear so it induces a B-linear map

$[\mathrm{Hom}_A(M, N)]^B \longrightarrow \mathrm{Hom}_B(M^B, N^B), \quad b \otimes f \mapsto b\cdot f^B,$

For this to be an isomorphism, we need to introduce a new concept.

Definition.

An A-module M is finitely presented if it is finitely generated, and for some surjective map $A^n \to M$ , its kernel is also finitely generated.

Note

In other words, M is finitely presented if and only if there is an exact sequence of the form

$A^m \to A^n \to M \to 0$ .

Intuitively, this means M can be described by a finite set of generators subjected to a finite set of relations.

Proposition 1.

If M is finitely presented, then the kernel K of any surjective map $A^n \to M$ is finitely generated.

Proof

Since M is finitely presented there is an exact sequence of the form $F_1 \to F_2 \to M \to 0$ where $F_1, F_2$ are finite free modules. Since $F_1, F_2$ are free and hence projective, there exist $f:F_2 \to A^n$ , $g:F_1 \to K$ making the diagram commute.

proof_for_fp_modules

By the snake lemma we have an exact sequence

$0 = \mathrm{ker} 1_M \to \mathrm{coker } g \to \mathrm{coker } f \to \mathrm{coker } 1_M =0$ .

Thus $\mathrm{coker } g \cong \mathrm{coker } f$ is finitely generated. Furthermore, since $F_1$ is finite free $\mathrm{im } g$ is finitely generated. Since $\mathrm{im }g$ and $K/\mathrm{im } g$ are finitely generated so is K. ♦

Exercise A

1. Find a module M over a ring A which is finitely generated but not finitely presented.

2. Prove that a finitely generated projective module is finitely presented.

3. Prove that in a short exact sequence of A-modules $0\to N \to M \to P \to 0$ , if N and P are finitely presented, so is M.

Optional Extra

The concept of finitely presented modules can be generalized further.

Definition

We say that an A-module M is of type $FP_n$ if there is an exact sequence

$F_n \longrightarrow \ldots \longrightarrow F_1 \longrightarrow F_0 \longrightarrow M \longrightarrow 0$

where each $F_i$ is finite free.

Thus saying M is $FP_0$ means it is finitely generated and saying M is $FP_1$ means it is finitely presented. One can show more generally that if M has type $FP_n$ then the kernel of any surjection $F\to M$ has type $FP_{n-1}$ . However, this is outside our scope of discussion.

This has applications in non-commutative algebra, where we study (say) left modules over a non-commutative ring and consider their cohomological properties. For details, see GTM 87, Cohomology of Groups, by Kenneth S. Brown.

blue-lin

Hom Functor and Induced Module

Now our main result is as follows.

Proposition 2.

If M is finitely presented and B is A-flat, we have an isomorphism

$[\mathrm{Hom}_A(M, N)]^B \stackrel \cong \longrightarrow \mathrm{Hom}_B(M^B, N^B), \quad b \otimes f \mapsto b\cdot f^B.$

Proof

Pick an exact sequence of A-modules: $A^m \stackrel f\to A^n \stackrel g\to M\to 0$ . Since Hom is left-exact, for any A-module N we have an exact sequence of A-modules

$0 \longrightarrow \mathrm{Hom}_A (M, N) \stackrel {g^*} \longrightarrow \mathrm{Hom}_A(A^n, N) \stackrel {f^*} \longrightarrow \mathrm{Hom}_A(A^m, N).$

And since $B\otimes_A -$ is exact, we get an exact sequence of B-modules

$0 \longrightarrow [\mathrm{Hom}_A (M, N)]^B \stackrel {(g^*)^B} \longrightarrow [\mathrm{Hom}_A(A^n, N)]^B \stackrel {(f^*)^B } \longrightarrow [\mathrm{Hom}_A(A^m, N)]^B.$

Since tensor product is right-exact, we also get an exact sequence of B-modules

$B^m \stackrel{f^B}\longrightarrow B^n \stackrel{g^B} \longrightarrow M^B \longrightarrow 0.$

Again since Hom is left-exact, we get an exact sequence of B-modules

$0 \longrightarrow \mathrm{Hom}_B(M^B, N^B) \stackrel {(g^B)^*} \longrightarrow \mathrm{Hom}_B(B^n, N^B) \stackrel {(f^B)^*} \longrightarrow \mathrm{Hom}_B(B^m, N^B).$

But we have natural isomorphisms

$[\mathrm{Hom}_A(A^n, N)]^B \cong (N^n)^B \cong (N^B)^n \cong \mathrm{Hom}_B(B^n, N^B)$

which commute with $[\mathrm{Hom}_A(M, N)]^B \longrightarrow \mathrm{Hom}_B(M^B, N^B)$ . Hence this map is an isomorphism. ♦

blue-lin

F.P. ⇒ (Projectivity is Local)

Since localization is exact and naturally isomorphic to $S^{-1}A \otimes_A -$ , as a special case we obtain the following.

Corollary 1.

If M is finitely presented, then $S^{-1}\mathrm{Hom}_A(M, N) \cong \mathrm{Hom}_{S^{-1}A}(S^{-1}M, S^{-1}N)$ .

Now we are ready to prove the following result.

Proposition 3.

If M is a finitely presented A-module, then M is A-projective if and only if $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -projective for all maximal $\mathfrak m\subset A$ .

In summary, for a finitely presented module, projectivity is a local property.

Proof

(⇒) Let M be A-projective. For a maximal $\mathfrak m\subset A$ ; we wish to show $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -projective. Let $f :N_1 \to N_2$ be a surjective $A_{\mathfrak m}$ -linear map. Now f is A-linear, and since M is A-projective

$\mathrm{Hom}_A(M, N_1) \stackrel {f_*}\longrightarrow \mathrm{Hom}_A(M, N_2)$

is surjective. Since M is finitely presented and $(N_i)_{\mathfrak m} \cong N_i$ , we get a surjective:

$\mathrm{Hom}_{A_{\mathfrak m}}(M_{\mathfrak m}, N_1) \cong \mathrm{Hom}_A(M, N_1)_{\mathfrak m} \longrightarrow \mathrm{Hom}_A(M, N_2)_{\mathfrak m}\cong \mathrm{Hom}_{A_{\mathfrak m}}(M_{\mathfrak m}, N_2).$

(⇐) Suppose $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -projective for all maximal $\mathfrak m$ . To prove M is A-projective, let $f:N_1 \to N_2$ be a surjective A-linear map. We need to show

$\mathrm{Hom}_A(M, N_1) \stackrel {f_*} \longrightarrow \mathrm{Hom}_A(M, N_2)$

is surjective; equivalently, we need to show $(f_*)_{\mathfrak m}$ is surjective for all maximal $\mathfrak m$ . But this is just

$\mathrm{Hom}_{A_{\mathfrak m}}(M_{\mathfrak m}, (N_1)_{\mathfrak m}) \cong \mathrm{Hom}_A(M, N_1)_{\mathfrak m} \longrightarrow \mathrm{Hom}_A(M, N_2)_{\mathfrak m} \cong \mathrm{Hom}_{A_{\mathfrak m}}(M_{\mathfrak m}, (N_2)_{\mathfrak m})$

which is surjective because $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -projective. ♦

blue-lin

Posted in Advanced Algebra | Tagged finitely presented, hom functor, induced modules, local properties, projective modules, snake lemma | Leave a comment

Commutative Algebra 32

Posted on April 20, 2020 by limsup

Torsion and Flatness

Definition.

Let A be a ring and M an A-module; let $a\in A$ .

If $m\in M$ satisfies $am=0$ , we call it an $a$ –torsion element.

If $m\in M$ is an $a$ -torsion for some non-zero-divisor $a\in A$ we call it a torsion element.

M is said to be torsion-free if it has no torsion elements other than 0.

Note that a torsion element in A is the same as a zero-divisor.

Exercise A

Decide if each of the following is true or false.

A submodule of a torsion-free module is torsion-free.
A quotient module of a torsion-free module is torsion-free.
An intersection of torsion-free submodules of M is torsion-free.
A sum of torsion-free submodules of M is torsion-free.
A direct sum of torsion-free modules is torsion-free.
A direct sum of a torsion-free module and any module is torsion-free.

Now we wish to prove:

Lemma 1.

A flat module M over a ring A is torsion-free.

Proof

Let $a\in A$ be a non-zero-divisor. The injection $0 \to A \stackrel {a}\to A$ (where $a$ here means multiplication by $a$ ) gives an injection upon tensoring with M : $0 \to M \stackrel {a}\to M$ . Hence M has no a-torsion elements other than 0. ♦

Note

Eventually, we will see that for a principal ideal domain, the converse is true.

blue-lin

A Little Geometry

Let us give a geometric interpretation to lemma 1. Take the concrete example

$A = k[X] \longrightarrow k[X, Y, Z]/(XZ, YZ) = B.$

As an A-module, B has torsion since $X \cdot \overline Z = 0$ so it is not A-flat. The homomorphism corresponds to a morphism f from the variety $W = \{(x, y, z): xz = yz= 0\}$ to $V = \mathbb A^1$ by projecting onto the x-coordinate. We treat W as a collection of varieties parametrized by points on V, with $W_x = f^{-1}(x)$ .

graph_of_xz_yz_equals_zero

Note that when $x\ne 0$ , we have $W_x = \{(x, y, 0) : y \in k\} \cong \mathbb A^1$ . And when $x = 0$ , we have $W_0 = \{(0, y, z) : yz = 0\}$ , a union of two lines. On an intuitive level, this means $\lim_{x\to 0} W_x \ne W_0$ , although such a statement makes no sense here.

The idea is: if $k[V] \to k[W]$ is flat, then $W\to V$ gives a family of varieties “smoothly parametrized” by elements of V.

For our case, let us rephrase our statement so that it is more algebra-friendly. Let $U = V - \{0\}$ ; we get the restriction $f : f^{-1}(U) \to U$ where $f^{-1}(U) = \{(x, y, z) : x\ne 0, z=0, y\in k\}$ . Taking the Zariski closure in their respective spaces gives us

$W^\circ := \overline{f^{-1}(U)}= \{(x,y,0) : z=0\}\longrightarrow \overline U = V, \quad (x,y,0) \mapsto x$

which is now flat since $k[W^\circ] \cong k[X, Y]$ and the homomorphism of coordinate rings is $k[X]\hookrightarrow k[X, Y]$ . This extension is flat since it is free.

In a nutshell, the problem is that $f^{-1}(U)$ is not dense in W even though U is dense in V.

Exercise B

Let $f:W\to V$ be a morphism of k-varieties with corresponding

$f^* : A := k[V] \longrightarrow k[W] =: B.$

Pick an open subset $D(g) \subseteq V$ for $g\in k[V]$ ; recall $D(g) = \{v\in V: g(v) \ne 0\}$ .

Prove that $D(g)$ is dense in V if and only if g is not a zero-divisor.
Prove that $f^{-1}(D(g))$ is exactly $D(f^*(g))$ .

Hence $D(g)$ and $f^{-1}(D(g))$ have coordinate rings $k[V][\frac 1 g]$ and $k[W][\frac 1 g]$ respectively. The geometric condition “if $D(g)$ is dense in V then $f^{-1}(D(g))$ is dense in W” then translates to “if $g\in k[V]$ is not a zero-divisor then $k[W]$ has no g-torsion”.

blue-lin

Examples

We will work through some concrete examples now.

Example 1

We have a sequence of flat extensions $A \subset A[X] \subset A[X, \frac 1 X]$ . The first inclusion is flat because $A[X]$ is free over A; the second inclusion is flat because it is a localization. By transitivity of flatness (proposition 3 here) we see that $A[X, \frac 1 X]$ is a flat A-algebra.

Example 2

The injection $k[X] \subset k[X, Y]/(XY)$ is not flat because X becomes a zero-divisor in $k[X, Y]/(XY)$ .

But what about the map $k[X, Y]/(XY) \to k[X]$ taking $Y\mapsto 0$ ? This is also not A-flat. For that we note that $k[X]$ is the quotient of $k[X, Y]/(XY)$ by the ideal (Y). Now apply the following lemma.

Lemma 2.

Let $\mathfrak a$ be an ideal of ring A. If $A/\mathfrak a$ is A-flat, then $\mathfrak a = \mathfrak a^2$ .

Proof

Take the exact sequence of A-modules $0 \to \mathfrak a \to A \to A/\mathfrak a \to 0$ . Taking $(A/\mathfrak a) \otimes_A -$ gives us, together with $(A/\mathfrak a) \otimes_A (A/\mathfrak a) \cong A/\mathfrak a$ , we get the exact sequence

$0 \longrightarrow \mathfrak a/\mathfrak a^2 \longrightarrow A/\mathfrak a \stackrel {\text{id.}} \longrightarrow A/\mathfrak a \longrightarrow 0.$

Hence $\mathfrak a / \mathfrak a^2 = 0$ . ♦

Now applying this to our case, we see that $(Y) \ne (Y^2)$ since $Y \in (Y) - (Y^2)$ .

Exercise C

Find an ideal $\mathfrak a \ne 0, (1)$ of a ring A which satisfies $\mathfrak a = \mathfrak a^2$ . For further challenge, give two different constructions.

Example 3

Take the affine k-varieties (k algebraically closed) $V = \{ (x,y) \in \mathbb A^2 : y^2 = x^3\}$ and $W = \mathbb A^1$ with $W\to V$ , $t \mapsto (t^2, t^3)$ , which corresponds to

$A = k[X, Y]/(Y^2 - X^3) \longrightarrow k[T] = B, \quad X \mapsto T^2, Y \mapsto T^3.$

We claim that B is not a flat A-algebra. There are a few ways to see this.

Direct Proof

Let $\mathfrak m = (X, Y) \subset A$ be a maximal ideal. It suffices to show that the product map $\mathfrak m \otimes_A B \to \mathfrak m B$ not injective. Indeed $X \otimes T^2, Y\otimes T$ both map to $T^2 \cdot T^2 = T^3 \cdot T = T^4$ . On the other hand, they are distinct elements of $\mathfrak m\otimes_A B$ . To see why we take

$(A/ \mathfrak m) \otimes_A \mathfrak m \otimes_A B \cong \mathfrak m /\mathfrak m^2 \otimes_A B,$

and the action of A on $\mathfrak m/\mathfrak m^2$ factors through $A/\mathfrak m$ . Since $\mathfrak m/\mathfrak m^2$ has basis X, Y (see the calculations from earlier) the above module is a direct sum of $(k\cdot X \otimes_A B)$ and $(k\cdot Y \otimes_A B)$ ; in particular $X\otimes T^2 \ne Y\otimes T$ in $\mathfrak m \otimes_A B$ .

Indirect Proof

If $A\to B$ is flat, then so is $A/(X) \to B/(X)B$ . But $X\mapsto T^2 \in B$ so the resulting map is

$k[X, Y]/(Y^2 - X^3, X) \cong k[Y]/(Y^2) \longrightarrow k[T]/(T^2), \quad Y \mapsto 0$ .

This map factors through $k[Y]/(Y^2) \to k \hookrightarrow k[T]/(T^2)$ . The first map is not flat by applying lemma 2 to the ideal $\mathfrak a = (Y)$ of ring $A' = k[Y]/(Y^2)$ . Specifically the injective map $\mathfrak a\to A'$ , upon applying the functor $(A'/\mathfrak a)\otimes_{A'} -$ , gives us $\mathfrak a \to k$ taking $Y\mapsto 0$ . Since $k[T]/(T^2)$ is free over k, upon applying $k[T]/(T^2) \otimes_k -$ , the map is still not injective.

Example 4

We consider a family of ellipses $\{x,y\in \mathbb A^2 : ax^2 + by^2 = c\}$ parametrized by a, b, c from earlier. This corresponds to the homomorphism

$f : k[A, B, C] \hookrightarrow k[A, B, C, X, Y]/(AX^2 + BY^2 - C)$ .

We claim that this is not flat. Using the trick in the indirect proof above, we factor by B = C = 0. It suffices to show that

$f' : k[A] \hookrightarrow k[A, X, Y]/(AX^2)$

is not flat. But $X \in \text{ RHS}$ is an A-torsion element, so we are done.

Geometrically, the ellipse degenerates at the point A = B = C = 0, so it becomes the whole plane.

Exercise D

1. Is the extension $k[T] \hookrightarrow k[X, Y, T]/(Y - TX^2)$ a flat extension? What if we restrict to $T\ne 0$ ?

2. Apply the same analysis to $k[T] \hookrightarrow k[X,Y,T]/(XY - T)$ .

3. For example 4, prove that the extension is flat if we restrict to the open affine subset $B \ne 0$ , i.e. we get the extension

$k[A, B, C, \frac 1 B] \hookrightarrow k[A, B, C, \frac 1 B, X, Y]/(AX^2 + BY^2 - C)$ .

Intuitively, this means if $b\ne 0$ , the family of ellipses $ax^2 + by^2 = c$ is well-behaved. What about the open subset $C\ne 0$ ?

blue-lin

Posted in Advanced Algebra | Tagged algebraic geometry, flat modules, torsion, varieties, zero-divisors | Leave a comment

Commutative Algebra 31

Posted on April 19, 2020 by limsup

Flat Modules

Recall from proposition 3 here: for an A-module M, $M \otimes_A -$ is a right-exact functor.

Definition.

We say M is flat over A (or A-flat) if $M\otimes_A -$ is an exact functor, equivalently, if

$N_1\stackrel f \longrightarrow N_2 \text{ injective } \implies M\otimes_A N_1\stackrel {1_M \otimes f} \longrightarrow M\otimes_A N_2 \text{ injective. }$

A flat A-algebra is an A-algebra which is flat as an A-module.

We say a ring homomorphism $f:A\to B$ is flat if the resulting A-algebra structure on B is flat.

Flat modules and algebras are a little hard to get a handle on, so we will first go through some properties before offering a few examples.

Proposition 1.

If $(M_i)$ is a collection of A-flat modules, then $\oplus_i M_i$ is A-flat.

Conversely, if $M\oplus N$ is flat, so is $M$ .

Proof

This follows from the natural isomorphism in N:

$\left(\oplus_i M_i \right) \otimes_A N \cong \oplus_i (M_i \otimes_A N).$ ♦

Proposition 2.

The localized ring $S^{-1}A$ is A-flat. In particular, A is A-flat.

Proof

We have the natural isomorphism in M given by $S^{-1}A \otimes_A M \cong S^{-1}M$ . Then use the fact that localization functors are exact (theorem 1 here). ♦

Corollary 1.

A free module is flat. More generally, a projective module is flat.

Proof

Since A is flat, by proposition 1, any free module $A^{\oplus I}$ is also flat.

If P is projective, $P \oplus Q$ is free for some A-module Q. Thus $P \oplus Q$ is flat. By proposition 1 again, P is flat. ♦

Proposition 3.

If B is a flat A-algebra and M is a flat B-module, then M is a flat A-module.

In particular, if C is a flat B-algebra and B is a flat A-algebra, then C is a flat A-algebra.

Proof

Indeed, we have a natural isomorphism for any A-module N:

$M\otimes_A N \cong M\otimes_B (B \otimes_A N).$ ♦

Exercise A

Prove the following.

If M, N are A-flat, so is $M\otimes_A N$ .
If M is a flat A-module, so is $S^{-1}M$ .
If M is A-flat, then $M^B = B\otimes_A M$ is B-flat for any B-algebra.

As a special case of the last property, we have:

$M \text{ is } A\text{-flat} \implies \begin{cases}S^{-1}M \text{ is } S^{-1}A\text{-flat} \\ M/\mathfrak a M \text{ is } A/\mathfrak a\text{-flat}.\end{cases}$

for any multiplicative subset $S\subseteq A$ and ideal $\mathfrak a \subseteq A$ .

Summary.

The above properties can be summarized as follows.

Flatness is preserved by direct sum and decomposition.

Localization is flat.

Projective modules are flat.

Flatness is transitive.

Note

The property of flatness may seem mysterious and obscure for the first-time reader. Roughly speaking, flat algebras can be interpreted geometrically as follows: if $A\to B$ is a flat ring homomorphism, the fibres $B\otimes_A k(\mathfrak p)$ maintain some consistency over various $\mathfrak p$ . We will see some concrete examples in the next article.

blue-lin

Flatness is Local

Before we state and prove the local properties, first recall that tensor product commutes with localization:

$(S^{-1}M) \otimes_{S^{-1}A} (S^{-1}N) \cong S^{-1}(M\otimes_A N).$

Also we need the following.

Lemma 1.

If $N$ is an $S^{-1}A$ -module and we treat it as an A-module, then $S^{-1}N \cong N$ as $S^{-1}A$ -modules.

Proof

Easy exercise. ♦

Local Property for A-Modules

Proposition 4.

Flatness is a local property, i.e. M is A-flat if and only if for each maximal ideal $\mathfrak m\subset A$ , $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -flat.

Proof

(⇒) Let M be A-flat; to show $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -flat let $f : N_1 \to N_2$ be an injective map of $A_{\mathfrak m}$ -modules. Now

$M_{\mathfrak m} \otimes_{A_{\mathfrak m}} N_i \cong M_{\mathfrak m} \otimes_{A_{\mathfrak m}} (N_i)_{\mathfrak m} \cong (M \otimes_A N_i)_{\mathfrak m}.$

Since M is A-flat, $1 \otimes f : M\otimes_A N_1 \to M\otimes_A N_2$ is injective, and hence so is $(M\otimes_A N_1)_{\mathfrak m}\to (M\otimes_A N_2)_{\mathfrak m}$ .

For (⇐) let $f : N \to N'$ be an injective homomorphism of A-modules. From corollary 2 here, $1_M \otimes f : M\otimes_A N \to M\otimes_A N'$ is injective if and only if $(1_M \otimes f)_{\mathfrak m}$ is injective for each $\mathfrak m$ . But this map is just:

$M_{\mathfrak m} \otimes_{A_{\mathfrak m}}N_{\mathfrak m} \cong (M\otimes_A N)_{\mathfrak m} \longrightarrow (M\otimes_A N')_{\mathfrak m} \cong M_{\mathfrak m} \otimes_{A_{\mathfrak m}}N'_{\mathfrak m},$

obtained by $1_{M_{\mathfrak m}} \otimes f_{\mathfrak m}$ . Since $M_{\mathfrak m}$ is $A_{\mathfrak m}$ -flat and $f_{\mathfrak m}$ is injective, we are done. ♦

Local Property for A-Algebras

Next, we have an even better result for A-algebras.

Proposition 5.

Let B be an A-algebra. B is A-flat if and only if for any maximal ideal $\mathfrak n \subset B$ and $\mathfrak p = \mathfrak n \cap A$ , the localization $B_{\mathfrak n}$ is $A_{\mathfrak p}$ -flat.

Note

$B_{\mathfrak n}$ is indeed an algebra over $A_{\mathfrak p}$ since any $s\in A - \mathfrak p$ is invertible in $B_{\mathfrak n}$ .

Proof

(⇒) $S^{-1}B$ is flat over $S^{-1}A$ . Now $B_{\mathfrak q}$ is a further localization of $S^{-1}B$ so it is flat over $S^{-1}B$ . Apply transitivity of flatness.

(⇐) Now suppose $B_{\mathfrak n}$ is flat over $A_{\mathfrak p}$ for all maximal $\mathfrak n$ and $\mathfrak p =\mathfrak n \cap A$ . Let $f : N_1\to N_2$ be an injective map of A-modules and let K be the kernel of $1_B \otimes f : B\otimes_A N_1 \to B \otimes_A N_2$ so we have an exact sequence of B-modules

$0 \longrightarrow K \longrightarrow B\otimes_A N_1 \stackrel {1\otimes f} \longrightarrow B\otimes_A N_2.$

For any maximal ideal $\mathfrak n \subset B$ we obtain an exact sequence

$0 \longrightarrow K_{\mathfrak n} \longrightarrow (B\otimes_A N_1)_{\mathfrak n} \stackrel {(1\otimes f)_{\mathfrak n}} \longrightarrow (B\otimes_A N_2)_{\mathfrak n}.$

But $(B\otimes_A N_i)_{\mathfrak n} \cong B_{\mathfrak n} \otimes_{A} N_i$ (exercise). And since $B_{\mathfrak n}$ is flat over $A_{\mathfrak p}$ and the latter is flat over A, by proposition 3 $B_{\mathfrak n}$ is flat over A. Thus $K_{\mathfrak n} = 0$ for all maximal $\mathfrak n\subset B$ and $K=0$ . ♦

blue-lin

Ideals and Submodules

Here are some results which are useful for determining when a module is not flat.

Lemma 2.

If M is A-flat, we get an isomorphism $\mathfrak a \otimes M\longrightarrow \mathfrak a M$ by multiplication.

Proof

Take the exact sequence $0 \to \mathfrak a \to A \to A/\mathfrak a \to 0$ of A-modules. Since tensoring is right-exact we get an exact sequence

$\mathfrak a \otimes M \longrightarrow M \longrightarrow M/\mathfrak a M \longrightarrow 0$ ,

where the first map is multiplication. If M is A-flat, the first map is injective; its image is clearly $\mathfrak a M$ . ♦

Note

In fact, the converse is true: if M is such that $\mathfrak a \otimes M \cong \mathfrak a M$ for all finitely generated ideals $\mathfrak a$ , then M is A-flat. But we will need more tools than what we have at the moment to prove this.

Now for any A-module M, we obtain a map as follows.

ideals_to_submodules

Such a map satisfies a few nice properties for all modules. Examples:

1. The zero ideal (resp. (1)) maps to the zero submodule (resp. M).

2. If $\mathfrak a\subseteq \mathfrak b$ , then $\mathfrak a M \subseteq \mathfrak b N$ .

3. We have $\mathfrak a (\mathfrak b M) = (\mathfrak {ab}) M$ .

4. For collection of ideals $(\mathfrak a_i)$ , we have $(\sum_i \mathfrak a_i)M = \sum_i (\mathfrak a_i M)$ .

When M is A-flat, we get many more. Lemma 2 tells us multiplication gives an isomorphism $\mathfrak a \otimes_A M \to \mathfrak a M$ . And since $\mathfrak -\otimes_A M$ is exact, we can apply many of the nice properties of exact functors.

5. For any ideals $\mathfrak a, \mathfrak b$ , we have $(\mathfrak a \cap \mathfrak b)M = \mathfrak a M \cap \mathfrak b M$ .

6. If $f : \mathfrak a \to \mathfrak b$ is an A-linear map of ideals, we obtain an induced A-linear $f_M : \mathfrak a M \to \mathfrak b M$ , $xm \mapsto f(x)m$ .

7. Let $\mathfrak c = \mathrm{ker } f$ ; then $\mathfrak c M = \mathrm{ker } f_M$ .

warning The above correspondence is neither injective nor surjective in general, even when M is A-flat. [Exercise: find a counter-example for each case.]

As a preview of (much) later chapters, when M is faithfully flat, the correspondence is injective.

Exercise B

Find an A-linear map $f:\mathfrak a \to \mathfrak b$ of ideals of A and an A-module M, such that the A-linear map $\mathfrak a M \to \mathfrak b M$ , $xm\mapsto f(x)m$ is not well-defined. Thus property 6 is non-trivial.

What can we say about the kernel of addition $\mathfrak a M \oplus \mathfrak b M \to (\mathfrak a + \mathfrak b) M$ ?

blue-lin

Posted in Advanced Algebra | Tagged direct sums, exact functors, flat modules, local properties, localization, projective modules, tensor products | Leave a comment

Commutative Algebra 30

Posted on April 17, 2020 by limsup

Tensor Product of A-Algebras

Proposition 1.

Let B, C be A-algebras. Their tensor product $D = B\otimes_A C$ has a natural structure of an A-algebra which satisfies

$(b \otimes c) \times (b'\otimes c') = (bb') \otimes (cc')$ .

Proof

Fix $(b, c) \in B \times C$ . The map $B\times C \longrightarrow B\otimes_A C, (b',c') \mapsto bb' \otimes cc'$ is A-bilinear so it induces an A-linear map

$m_{b,c} : B\otimes_A C \longrightarrow B\otimes_A C, \quad b'\otimes c' \mapsto bb' \otimes cc'.$

Now varying (b, c) gives an A-bilinear map $B\times C \to \mathrm{Hom}_A (B\otimes_A C, B\otimes_A C)$ , $(b, c) \mapsto m_{b,c}$ so it induces an A-linear

$B\otimes_A C \longrightarrow \mathrm{Hom}_A(B\otimes_A C, B\otimes_A C), \quad b\otimes c \mapsto (b' \otimes c' \mapsto bb' \otimes cc'),$

i.e. an A-bilinear map $D \times D \to D$ . Note that A-bilinearity means distributivity in either term. To prove associativity, show that it holds on the pure tensors (exercise). ♦

It turns out this is the coproduct of B and C in the category of A-algebras. This was briefly aluded to earlier.

Proposition 2.

Let $D = B\otimes_A C$ with A-algebra homomorphisms

$\begin{aligned} \phi_1 : B\longrightarrow B\otimes_A C, &\quad b \mapsto b\otimes 1_C, \\ \phi_2 : C \longrightarrow B\otimes_A C, &\quad c \mapsto 1_B \otimes c.\end{aligned}$

If E is an A-algebra and $\psi_1 : B \to E$ , $\psi_2 : C\to E$ are A-algebra homomorphisms, then there is a unique A-algebra homomorphism $f:D \to E$ such that $f\circ \phi_1 = \psi_1$ and $f\circ \phi_2 = \psi_2$ .

Proof

The A-bilinear map $B\times C\to E, (b,c) \mapsto \psi_1(b)\psi_2(c)$ induces the A-linear map

$f : B\otimes_A C\longrightarrow E, \quad b\otimes c\mapsto \psi_1(b) \psi_2(c)$ .

To check that it is a ring homomorphism, it suffices to take the pure tensors, and show that $f((b\otimes c)(b'\otimes c')) = f(b\otimes c)f(b'\otimes c')$ .

Clearly $f\circ\phi_i = \psi_i$ for $i =1,2$ , and conversely, any such f must satisfy $f(b\otimes c) = \psi_1(b) \psi_2(c)$ which uniquely determines f. ♦

blue-lin

Examples

1. Induced Algebra

In the above suppose we fix B and take the functor

$A\text{-}\mathbf{Mod} \longrightarrow B\text{-}\mathbf{Mod},\quad C \mapsto B\otimes_A C$

This functor satisfies the universal property: for any B-algebra D we have

$\mathrm{Hom}_{B\text{-alg}}(B\otimes_A C, D) \cong \mathrm{Hom}_{A\text{-alg}}(C, D).$

In fact, this is a general property from category theory.

Lemma 1.

If $B\in \mathcal C$ is an object, and $B\amalg C$ is the coproduct of B and C, then for each $f:B\to D$ in $\mathcal C$ we have a natural isomorphism

$\mathrm{hom}_{\mathcal C}(C, D) \stackrel\cong \longrightarrow \mathrm{hom}_{B \downarrow \mathcal C} (i_B, f),$

where $i_B : B\to B \amalg C$ is the canonical map and $B\downarrow \mathcal C$ is the coslice category.

Exercise A

Do at least one of the following.

Prove the universal property directly.
Prove the lemma and use it to prove the universal property.

2. Polynomial Ring

We have $B \otimes_A A[X] \cong B[X]$ for any A-algebra B. There is more than one way to show it.

Proof 1: use the fact that $A[X]$ is free over A with basis $X^n$ for $n\ge 0$ , so $B \otimes_A A[X]$ is free over B with the same basis. Show that product in this ring still satisfies $X^m \times X^n = X^{m+n}$ so it is isomorphic to $B[X]$ .

Proof 2: for any B-algebra C, example 1 gives

$\mathrm{Hom}_{B\text{-alg}}(B \otimes_A A[X], C) \cong \mathrm{Hom}_{A\text{-alg}}(A[X], C) \cong C$

as sets functorially in C. Since we also have $\mathrm{Hom}_{B\text{-alg}} (B[X], C)\cong C$ , the result follows by Yoneda lemma.

3. Localization

Let B be an A-algebra with given homomorphism $f:A\to B$ . If $S\subseteq A$ is a multiplicative subset, then $S^{-1}A \otimes_A B \cong S^{-1}B$ as A-modules as we saw earlier. Clearly the isomorphism preserves the ring structure so we get an isomorphism of A-modules.

Technically you have to localise with respect to a multiplicative subset of the ring, so it would be more correct to write $T^{-1}B$ where $T = f(S)$ .

What is $\mathrm{Spec} S^{-1}B$ ? This is the set of primes $\mathfrak q \subset B$ such that

$\mathfrak q \cap T = \mathfrak q \cap f(S) = \emptyset \iff f^{-1}(\mathfrak q) \cap S = \emptyset.$

In other words $\mathrm{Spec} (S^{-1}A \otimes_A B) = (f^*)^{-1} (\mathrm{Spec} S^{-1}A)$ under the continuous map $f^* : \mathrm{Spec} B \to \mathrm{Spec} A$ .

4. Quotient

Let B be an A-algebra with given homomorphism $f:A\to B$ . If $\mathfrak a \subseteq A$ is an ideal, then $(A/\mathfrak a)\otimes_A B \cong B/\mathfrak a B$ as A-modules. Again it is in fact an isomorphism of A-algebras. Now $\mathrm{Spec} B/\mathfrak a B$ is the set of primes $\mathfrak q$ such that

$\mathfrak q \supseteq \mathfrak a B \iff \mathfrak q \supseteq f(\mathfrak a) \iff f^{-1}(\mathfrak q) \supseteq \mathfrak a$ .

Thus $\mathrm{Spec} (A/\mathfrak a \otimes_A B) = (f^*)^{-1}(\mathrm{Spec} A/\mathfrak a)$ .

Exercise B

For ideals $\mathfrak a, \mathfrak b$ , describe $(A/\mathfrak a)\otimes_A (A/\mathfrak b)$ .

Let $B =A[X_1, \ldots X_n]/(f_i)$ where $f_i\in A[X_1, \ldots, X_n]$ is a collection of polynomials. Describe the functor $B\otimes_A -$ .

blue-lin

Geometric Applications

Throughout this section, k denotes an algebraically closed field.

Fibre of a Morphism

Let $f:A\to B$ be a ring homomorphism and $\mathfrak p \subset A$ be a prime ideal. Substitute $\mathfrak a = \mathfrak p$ in example 4 and $S = A - \mathfrak p$ in example 3. Thus the set of $\mathfrak q \in \mathrm{Spec} B$ such that $f^*(\mathfrak q) = f^{-1}(\mathfrak q) = \mathfrak p$ is given by:

$S^{-1}A \otimes_A (A/\mathfrak p) \otimes_A B \cong k(\mathfrak p) \otimes_A B$

where $k(\mathfrak p)$ is the residue field of A at $\mathfrak p$ .

Definition.

Let $\phi : V\to W$ be a morphism of affine k-schemes, which corresponds to a ring homomorphism $f :k[W] \to k[V]$ . For a given point $P\in W$ , its fibre is the affine k-scheme $\phi^{-1}(P)$ with coordinate ring:

$k[\phi^{-1}(P)] = (k[W]/\mathfrak m_P) \otimes_{k[W]} k[V] \cong k[V]/f(\mathfrak m_P) k[V].$

Example

Let $V = \{(a,b,c,x,y) \in \mathbb A^5 : ax^2 + by^2 = c\}$ and $W = \mathbb A^3$ with morphism $\phi:V \to W$ , $(a,b,c,x,y) \mapsto (a,b,c)$ . Algebraically, this is:

$f : k[A, B, C] \hookrightarrow k[A, B, C, X, Y]/(AX^2 + BY^2 - C)$ .

For the point $(1, 1, 1) \in W$ , we have $\mathfrak m = (A-1, B-1, C-1)$ so that

$\begin{aligned} k[\phi^{-1}(P)] &= k[A, B, C, X, Y]/(AX^2 + BY^2 - C, A-1, B-1, C-1)\\ &\cong k[X, Y]/(X^2 + Y^2 - 1).\end{aligned}$

The point $Q = (0, 0, 0)\in W$ , on the other hand, gives $k[\phi^{-1}(Q)] \cong k[X, Y]$ .

Geometrically, V is a family of ellipses parametrized by the parameters a, b, c.

Product of Varieties

Suppose $V\subseteq \mathbb A^n$ , $W\subseteq \mathbb A^m$ are closed subsets. Then $V\times W \subseteq \mathbb A^{m+n}$ is also closed, being cut out by the same equations which define V and W, but with disjoint sets of variables.

warning The topology for $V\times W$ is generally much finer than the product topology of V and W. For example, prove this for $V = W = \mathbb A^1$ as an easy exercise.

Lemma 2.

$k[V\times W] \cong k[V] \otimes_k k[W]$ .

Proof

The projection maps $V\times W \to V, W$ induce k-algebra homomorphisms $k[V], k[W] \to k[V\times W]$ and hence $h : k[V]\otimes_k k[W] \to k[V\times W]$ ; h is surjective by our concrete description of $V\times W$ above.

For injectivity, let S be a basis of $k[V]$ . Suppose $h(\sum_{i=1}^n f_i \otimes g_i)= 0$ for some $f_1, \ldots, f_n \in S$ and $g_1, \ldots, g_n \in k[W]$ . Thus

$v\in V, w\in W \implies \sum_{i=1}^n f_i(v) g_i(w) = 0$ .

If we fix w, we get a linear relation $\sum_{i=1}^n g_i(w) f_i = 0$ which holds in $k[V]$ . Since the $f_i$ ‘s are linearly independent, $g_1(w) = \ldots = g_n(w) = 0$ for all $w\in W$ so each $g_i = 0$ and $\sum_{i=1}^n f_i \otimes g_i = 0$ . ♦

Corollary 1.

If k is an algebraically closed field and A, B are finitely generated reduced k-algebras, then so is $A\otimes_k B$ .

Proof

Indeed A, B are isomorphic to k[V], k[W] for some k-varieties V and W. Apply the above. ♦

Exercise C

Find a counter-example when k is not algebraically closed. [ Hint: you need a base field of positive characteristic. ]

Intersection

Finally, we leave the following as an exercise.

Exercise D

Let $W_1, W_2$ be closed subvarieties of a variety V. This induces surjective k-algebra homomorphisms $k[V] \to k[W_1]$ and $k[V] \to k[W_2]$ . Write down the coordinate ring of the scheme intersection $W_1 \cap W_2$ using the language of tensor product.

Question to Ponder

Intuitively, there seems to be some commonality among the above three constructions. Explain this in terms of category theory. [ Hint: you might want to wait until the article on fibre products. ]

blue-lin

Posted in Advanced Algebra | Tagged algebraic geometry, algebras, coproducts, fibres, tensor product, varieties | 2 Comments

Commutative Algebra 29

Posted on April 16, 2020 by limsup

Distributivity

Finally, tensor product is distributive over arbitrary direct sums.

Proposition 1.

Given any family of modules $(N_i)_{i\in I}$ , we have:

$M \otimes_A \left( \oplus_{i\in I} N_i\right) \cong \oplus_{i\in I} (M\otimes_A N_i).$

Proof

Take the map $M \times (\oplus_i N_i) \to \text{ RHS }$ which takes $(m, (n_i)_{i\in I}) \mapsto (m \otimes n_i)_{i \in I}$ . Note that this is well-defined: since only finitely many $n_i$ are non-zero, only finitely many $m\otimes n_i$ are non-zero. It is A-bilinear so we have an induced A-linear map

$f : M\otimes_A (\oplus_i N_i) \longrightarrow \oplus_{i\in I} (M\otimes_A N_i), \quad m \otimes (n_i)_{i\in I} \mapsto (m\otimes n_i)_{i\in I}.$

The reverse map is left as an exercise. ♦

Example

Let us prove that the first example of the previous article is truly the tensor product of V and W. More generally suppose M (resp. N) is a finite free module over A with basis $e_1, \ldots, e_n$ (resp. $f_1, \ldots, f_m)$ . Write $M \cong A^{\oplus n}$ and $N \cong A^{\oplus m}$ . Distributivity together with $A\otimes_A A \cong A$ gives us:

$M\otimes_A N \cong \overbrace{(A \oplus\ldots \oplus A)}^{n \text{ terms}} \otimes \overbrace{(A \oplus\ldots \oplus A)}^{m \text{ terms}} \cong A^{\oplus mn}$

with basis given by $e_i \otimes f_j$ over $1 \le i \le n, 1 \le j \le m$ . More generally:

Corollary 1.

We have $\left(A^{\oplus I}\right) \otimes \left(A^{\oplus J}\right) \cong \left(A^{\oplus I \times J}\right)$ , i.e. a tensor product of free modules is free.

Exercise A

Prove that a tensor product of two projective modules is projective.

Note

Recall that localization commutes with arbitrary direct sums; tensor product also commutes with arbitrary direct sums. Does that mean tensor product commutes with localization? The answer is yes: the reader should be able to prove this as an easy exercise by the end of this article.

Summary.

We imagine the class of A-modules as having a “semi-ring”-like structure, where

A ↔ multiplicative identity;

direct sum ↔ addition;

tensor product ↔ multiplication.

blue-lin

⊗ is Right-Exact

First, we re-interpret the universal property of tensor product as follows.

Proposition 2.

For any A-modules M, N, P, we have a natural isomorphism of A-modules

$\begin{aligned}\mathrm{Hom}_A(M\otimes_A N, P) &\cong \mathrm{Hom}_A(M, \mathrm{Hom}_A (N, P)), \\ \phi &\mapsto (m \mapsto (n \mapsto \phi(m\otimes n)),\end{aligned}$

where both sides are treated as functors in M, N and P (contravariant in M, N, covariant in P).

Proof

Indeed, the universal property of tensor product says: the LHS corresponds to the set of all bilinear maps $B : M\times N\to P$ where $\phi$ corresponds to $B(m, n) = \phi(m\otimes n)$ . Clearly B corresponds to a linear map $M \to \mathrm{Hom}_A(N, P)$ , via $m\mapsto (n \mapsto B(m, n))$ . Hence we get the desired bijection. It is easy to show that the map is A-linear. ♦

Let M be an A-module; recall that $M\otimes -$ is functorial.

Proposition 3.

The functor $M\otimes_A -$ is a covariant right-exact functor.

Proof

Additivity is left as a simple exercise. To prove right-exactness, let $N_1 \stackrel f\to N_2 \stackrel g \to N_3 \to 0$ be an exact sequence.

To show that $M\otimes_A N_1 \stackrel {1_M \otimes f} \longrightarrow M\otimes_A N_2 \stackrel {1_M \otimes g} \longrightarrow M\otimes_A N_3 \longrightarrow 0$ is exact, by proposition 4 here it suffices to show that for any A-module P,

$0 \to \mathrm{Hom}_A(M \otimes_A N_3, P) \stackrel {(1 \otimes g)^*}\longrightarrow \mathrm{Hom}_A(M \otimes_A N_2, P) \stackrel {(1\otimes f)^*}\longrightarrow \mathrm{Hom}_A(M \otimes_A N_1, P)$

is exact. But by the previous result, this sequence is isomorphic to

$0\longrightarrow \mathrm{Hom}_A (M, \mathrm{Hom}_A(N_3, P)) \longrightarrow \mathrm{Hom}_A (M, \mathrm{Hom}_A(N_2, P)) \longrightarrow \mathrm{Hom}_A (M, \mathrm{Hom}_A(N_1, P)).$

Now we know this is exact by apply left-exactness of the Hom functor twice, once for $\mathrm{Hom}_A(-, P)$ and once for $\mathrm{Hom}_A(M, -)$ . ♦

blue-lin

Induced B-Modules

Let B be an A-algebra.

Definition.

Given an A-module M, we write $M^B := B\otimes_A M$ .

The notation is identical to our earlier one for induced modules, for a good reason.

Proposition 4.

Let $\phi : M\to M^B = B\otimes_A M$ be defined by $m\mapsto 1_B\otimes m$ . Then $(M^B, \phi)$ is the induced module.

Note

Let us refresh the reader’s memory: we want to show that for any B-module N and A-linear $\psi : M\to N$ , there is a unique B-linear $f:M^B \to N$ such that $f\circ \phi = \psi$ .

Proof (with bug)

Consider the map $B \times M \to N$ which takes $(b,m) \mapsto b\cdot \psi(m)$ . This is clearly A-bilinear so it induces an A-linear $f : B\otimes_A M \to N$ which takes $b\otimes m \mapsto b\cdot\psi(m)$ . It follows that $f(\phi(m)) = f(1\otimes m) = \psi(m)$ .

For uniqueness of f, by condition $f(1\otimes m) = f(\phi(m)) = \psi(m)$ ; since f is B-linear, $f(b\otimes m) = b\cdot f(1\otimes m) = b\cdot \psi(m)$ . Since every element of $B\otimes_A M$ is a finite sum of $b\otimes m$ we see that f must be as defined above. ♦

Important Exercise

The above proof has a huge bug in it. Find it and fix it.

[Hint: in the first paragraph, we did not prove that f is B-linear. But for that, we need M^B to have the structure of a B-module, which we forgot to define… ]

blue-lin

Special Cases

The various constructions we have seen for modules are actually induced. Thus $M\mapsto M^B$ is a generalization of these cases we have already seen.

1. Localization

Proposition 5.

We have a natural isomorphism

$S^{-1}A \otimes_A M \cong S^{-1}M, \quad \frac a s \otimes m \mapsto \frac{am}s.$

Proof

Take the A-bilinear map $S^{-1}A \times M \to S^{-1}M$ , by $(\frac a s, m) \mapsto \frac{am}s$ . Show that this is well-defined (i.e. independent of choice of a and s). So we get an A-linear map $S^{-1}A \otimes_A M \to S^{-1}M$ as above.

For the reverse map we take $S^{-1}M \to S^{-1}A \otimes_A M$ via $\frac m s \mapsto \frac 1 s \otimes_A m$ . To show this is well-defined, if $\frac m s = \frac {m'}{s'}$ then $ts'm = tsm'$ for some $t\in S$ which gives

$\frac 1 s \otimes_A m = \frac {s't}{ss't} \otimes_A m = \frac 1 {ss't} \otimes_A s'tm = \frac 1 {ss't} \otimes_A stm' = \frac {st}{ss't} \otimes_A m' = \frac 1 {s'} \otimes_A m'$ .

Both maps are clearly mutually inverse.

2 Quotient

Let $\mathfrak a\subseteq A$ be an ideal.

Proposition 6.

We have a natural isomorphism

$(A/\mathfrak a) \otimes_A M \cong M/\mathfrak a M$ .

Note

Hence, together with right-exactness of tensor product, we recover the earlier result (corollary 2 here) that $M\mapsto M/\mathfrak a M$ is right-exact.

Sketch of Proof

Define an A-linear map $f:(A/\mathfrak a) \otimes_A M \to M/\mathfrak a M$ which takes $\overline a \otimes m \mapsto \overline {am}$ . Also define the reverse map $g : M/\mathfrak a M\to (A/\mathfrak a)\otimes_A M$ by $\overline m\mapsto \overline 1 \otimes m$ . ♦

Exercise B

Fill in the details.

3 Polynomial (Exercise C)

Given $B = A[X]$ and an A-module M, describe the induced A[X]-module $B\otimes_A M$ .

blue-lin

Properties

The construction $M\mapsto M^B$ is functorial.

induced_modules

Indeed if $f:M\to N$ is A-linear, let $\phi_M : M\to M^B$ and $\phi_N : N \to N^B$ be the maps in the universal property. We leave it to the reader to fill out the remainder of the proof to obtain a B-linear $f^B : M^B \to N^B$ .

It is also additive and right-exact, as we saw earlier.

Exercise D

Find an A-algebra B and an injective A-linear map $f:M\to N$ of A-modules such that $f^B : M^B \to N^B$ is not injective.

Proposition 7.

Module induction is transitive. Thus if C is a B-algebra and B is an A-algebra then

$C \otimes_B (B\otimes_A M)\cong C \otimes_A M, \quad c \otimes_B (b\otimes_A m) \mapsto bc \otimes_A m,$

as an isomorphism of C-algebras.

Proof

Apply Yoneda lemma. For any C-module N we have a series of natural isomorphisms

$\begin{aligned} \mathrm{Hom}_C ( C\otimes_B (B\otimes_A M), N) &\cong \mathrm{Hom}_B(B\otimes_A M, N) \\ &\cong \mathrm{Hom}_A(M, N) \\ &\cong \mathrm{Hom}_C( C\otimes_A M, N)\end{aligned}$

so $C\otimes_A M \cong C\otimes_B (B\otimes_A M)$ as C-modules. ♦

The earlier general properties of tensor product further imply the following.

Properties of Induced B-Module.

We have $A^B \cong B$ .

For any family of A-modules $(M_i)_{i\in I}$ we have

$\left( \oplus_{i\in I} M_i \right)^B \cong \oplus_{i\in I} (M_i)^B.$

Given A-modules M and N, we have

$M^B \otimes_B N^B \cong (M \otimes_A N)^B.$

Proof

In each case, the earlier properties imply we have an isomorphism of A-modules on both sides. E.g. for the last case we have:

$M^B \otimes_B N^B \cong (B\otimes_A M) \overbrace{\otimes_B (B}^{\text{cancel}}\otimes_A N)\cong (B\otimes_A M) \otimes_A N \cong B\otimes_A (M\otimes_A N).$

Now to check that the maps are actually B-linear, we let $b\in B$ act on the pure tensors on both sides and show that they match. E.g. for the last case, the isomorphism takes $(b\otimes_A m) \otimes_B (b' \otimes_A n) \mapsto bb' \otimes_A m \otimes_A n$ . Multiplying both sides by $b''\in B$ gives:

commutative_diagram_tensor_induced

Since every element of $M^B \otimes_B N^B$ is a finite sum of $(b\otimes_A m) \otimes_B (b' \otimes_A n)$ , the result follows. ♦

blue-lin

Posted in Advanced Algebra | Tagged hom functor, induced modules, localization, right-exact, tensor products, yoneda lemma | 2 Comments

Commutative Algebra 28

Posted on April 15, 2020 by limsup

Tensor Products

In this article (and the next few), we will discuss tensor products of modules over a ring. Here is a motivating example of tensor products.

Example

If $V = \{a + bx + cx^2 : a,b,c \in \mathbb R\}$ and $W = \{a' + b'y + c'y^2 : a', b', c' \in \mathbb R\}$ are real vector spaces, then $V\otimes_{\mathbb R} W$ is the vector space with basis $x^i y^j$ over $0 \le i \le 2, 0 \le j \le 2$ . Hence it follows that $\dim (V\otimes W) = \dim V \times \dim W$ .

Also $\mathbb C \otimes_{\mathbb R} V$ is the complex vector space of all $a+bx+cx^2$ where $a,b,c\in \mathbb C$ . Thus $\dim_{\mathbb C} (\mathbb C\otimes_{\mathbb R} V) = \dim_{\mathbb R} V$ .

These properties will be proven as we cover the theory.

Throughout this article, A is a fixed ring and all modules and linear maps are over A.

Definition.

Given modules M, N, P, an A-bilinear map is a function

$B : M\times N \longrightarrow P$

such that:

for each $m\in M$ , the function $B(m, -) : N\to P$ is A-linear;

for each $n\in N$ , the function $B(-, n) : M\to P$ is A-linear.

For example over the base ring $\mathbb Z$ , the Euclidean inner product

$\mathbb Z^n \times \mathbb Z^n \longrightarrow \mathbb Z, \quad ((x_1, \ldots, x_n), (y_1, \ldots, y_n)) \mapsto \sum_i x_i y_i$

is bilinear. It is important to distinguish between a bilinear $M\times N\to P$ and a linear $M\times N\to P$ . For example, in a bilinear map, we must have $B(m, 0) = 0$ for all $m\in M$ while this is hardly ever true for a linear map.

Philosophically, we want the tensor product of M and N to be the module that classifies all bilinear maps from $M\times N$ .

Definition.

The tensor product of modules M, N comprises of:

$(P, \phi : M\times N \to P)$

where $P = M\otimes_A N$ is a module, $\phi$ is a bilinear map, such that for any pair

$(Q, \psi : M\times N \to Q)$

where Q is a module and $\psi$ is bilinear, there is a unique linear map $f : P \to Q$ such that $f\circ\phi = \psi$ .

Exercise A

1. Prove that the tensor product is unique up to unique isomorphism.

2. For our initial example of $V\otimes_{\mathbb R} W$ , let X be the space of all $a+bx$ with a, b real. Now take the bilinear

$V \times W \longrightarrow X, \quad (f(x), g(y)) \mapsto f(1)g(-1) + \frac{df}{dx} g(1).$

Compute the resulting $V\otimes_{\mathbb R} W \to X$ .

blue-lin

Construction

To prove that the tensor product exists for any A-modules M and N, let $F$ be the free A-module generated by $M\times N$ as a set. The standard basis of F is denoted by $e_{m, n}$ for $(m,n) \in M\times N$ . Now let P be the quotient of F by the submodule generated by elements of the form:

$\begin{aligned} e_{m+m', n} - e_{m,n} - e_{m', n}, &\quad e_{am, n} - a\cdot e_{m, n},\\ e_{m, n+n'} - e_{m,n} - e_{m,n'}, &\quad e_{m,an} - a\cdot e_{m,n},\end{aligned}$

over all $m,m'\in M, n, n'\in N, a\in A$ . The map $\phi : M\times N \to P$ is defined by $(m, n) \mapsto \overline e_{m,n}$ ; by definition of P this is A-bilinear.

Lemma.

The pair $(P, \phi:M\times N\to P)$ forms the tensor product of M and N.

Proof

Let Q be any module and $\psi : M\times N\to Q$ be any bilinear map. We first define a linear $f': F \to Q$ by taking $e_{m, n}\mapsto \psi(m, n)$ . This map factors through P because:

by bilinearity of $\psi$ we have $\psi(m + m', n) - \psi(m, n) - \psi(m', n) = 0$ and thus $f'$ takes $e_{m+m', n} - e_{m,n} - e_{m',n}$ to 0; Similarly it also takes all elements of the form $e_{am, n} - a\cdot e_{m, n}$ , $e_{m, n+n'} - e_{m,n} - e_{m,n'}$ and $e_{m,an} - a\cdot e_{m,n}$ to zero.

Hence we obtain a linear $f:P \to Q$ which takes $\overline e_{m,n} \mapsto \psi(m, n)$ . We have

$f\circ\phi(m,n) = f(\overline e_{m,n}) = \psi(m,n)$

and so $f\circ\phi = \psi$ .

To prove f is unique, since $f\circ \phi = \psi$ we must have $f(\overline e_{m,n}) = f(\phi(m,n)) = \psi(m,n)$ . But the set of $\overline e_{m,n}$ generates F so this proves uniqueness. ♦

Note

Let us set some notation. For the given $\phi : M\times N\to M\otimes N$ , any $m\in M$ and $n\in N$ gives us $\phi(m, n)$ , denoted by $m\otimes_A n$ . The universal property of tensor product thus says the following.

Any A-bilinear $\psi : M\times N\to Q$ induces a unique linear $M\otimes_A N\to Q$ which sends $m\otimes_A n\mapsto \psi(m, n)$ .

From the explicit construction of the tensor product, we also have:

Corollary 1.

The module $M\otimes_A N$ is generated by $m\otimes_A n$ over all $m\in M$ and $n\in N$ .

warning Every element of $M\otimes_A N$ is thus a sum of various $m\otimes n$ ; but in general not every element is of the form $m\otimes n$ . Counter-examples should be easy to find if you take $V\otimes_{\mathbb R} W$ in the beginning of this article.

Exercise B

Prove functoriality: if $f:M\to M'$ and $g:N\to N'$ are linear maps, they induce a linear $h: M\otimes_A N \to M'\otimes_A N'$ satisfying $h(m\otimes n) = f(m) \otimes g(n)$ . We denote this map by $f\otimes g$ .

In other words, we get a covariant functor

$\otimes : A\text{-}\mathbf{Mod} \times A\text{-}\mathbf{Mod} \longrightarrow A\text{-}\mathbf{Mod}$

warning Even if f is injective, $f\otimes 1_N : M\otimes_A N \to M'\otimes_A N$ is not injective in general. Thus the functor $- \otimes_A N$ does not take injective maps to injective maps. An example will be given at the end of this article.

blue-lin

Basic Properties

Now we prove some basic properties of the tensor product.

Proposition 1.

For any module M, $A\otimes_A M \cong M$ , where $a\otimes m\mapsto am$ .

Note

The isomorphism is natural. To be exact, both sides are functorial in M and we get a natural isomorphism between the functors.

Proof

Let us construct A-linear maps

$f:A\otimes_A M \to M, \quad g : M\to A\otimes_A M.$

To define f we take the map $A\times M\to M$ , $(a, m) \mapsto am$ . This is easily checked to be A-bilinear so it induces an $f: A\otimes_A M \to M$ satisfying $f(a\otimes m) = am$ .

Defining g is easy: set $g(m) = 1 \otimes m$ , which is A-linear. It remains to show the maps are mutually inverse. Let $a\in A$ , $m\in M$ .

We have $g(f(a \otimes m)) = g(am) = 1 \otimes am = a\otimes m$ due to bilinearity. Since the pure tensors $a\otimes m$ generate $A\otimes_A M$ we have $g\circ f = 1$ .
Also $f(g(m)) = f(1\otimes m) = m$ so $f\circ g = 1$ too. ♦

Proposition 2.

For any modules M, N, P, we have

$(M\otimes_A N)\otimes_A P \cong M\otimes_A (N\otimes_A P), \quad (m\otimes n) \otimes p \mapsto m\otimes (n\otimes p).$

Note

Again, this isomorphism is functorial in M, N and P.

Proof

Fix $m\in M$ and consider the map $\phi_m : N\times P \to (M\otimes_A N)\otimes_A P$ which takes $(n, p) \mapsto (m\otimes n)\otimes p$ . This is an A-bilinear map so it induces a linear

$f_m : N\otimes_A P \longrightarrow (M\otimes_A N)\otimes_A P, \quad (n\otimes p) \mapsto (m\otimes n) \otimes p.$

Now the map $\phi : M \times (N\otimes P) \to (M\otimes_A N)\otimes_A P,$ which takes $(m, x) \mapsto f_m(x)$ is A-bilinear so it induces a linear

$f : M\otimes_A (N \otimes_A P) \longrightarrow (M\otimes_A N)\otimes_A P, \quad m\otimes(n \otimes p) \mapsto (m\otimes n)\otimes p.$

Similarly, we can define a linear $g : (M\otimes_A N)\otimes_A P \to M\otimes_A (N \otimes_A P)$ which takes $(m\otimes n)\otimes p \mapsto m\otimes (n \otimes p)$ . Thus $g\circ f$ takes elements of the form $m\otimes (n\otimes p)$ back to themselves; since these generate the whole module we have $g\circ f = 1$ . Similarly $f\circ g = 1$ . ♦

Proposition 3.

For any modules M, N, we have

$M\otimes_A N \cong N\otimes_A M, \quad (m\otimes n) \mapsto (n\otimes m).$

Proof

Exercise. ♦

Example

Consider $\mathbb Z \stackrel 2\to \mathbb Z$ , the multiplication-by-2 map. Taking $- \otimes_{\mathbb Z} (\mathbb Z/2\mathbb Z)$ gives us $\mathbb Z/2\mathbb Z \to \mathbb Z/2\mathbb Z$ , still multiplication-by-2 but now it is the zero map. Hence tensor products do not take injective maps to injective maps in general.

blue-lin

Posted in Advanced Algebra | Tagged bilinear maps, distributive property, modules, tensor product, universal properties | 2 Comments

Artinian Modules

Examples

Simple Modules

Composition Series

Uniqueness of Composition Series

Irreducible Spaces

Noetherian Topological Spaces

Irreducible Components

Components of Noetherian Space

Geometric Interpretation

Example

Noetherian Modules

Classification of Noetherian Modules

Constructing Noetherian Rings

Hilbert Basis Theorem

Nakayama’s Lemma

Cotangent Spaces

Example 1

Example 2

Example 3

F. P. + Flat = F. G. + Projective

Snake Lemma

Finitely Presented Modules

Optional Extra

Hom Functor and Induced Module

F.P. ⇒ (Projectivity is Local)

Torsion and Flatness

A Little Geometry

Examples

Example 1

Example 2

Example 3

Example 4

Exercise D

Flat Modules

Flatness is Local

Local Property for A-Modules

Local Property for A-Algebras

Ideals and Submodules

Tensor Product of A-Algebras

Examples

1. Induced Algebra

2. Polynomial Ring

3. Localization

4. Quotient

Geometric Applications

Fibre of a Morphism

Product of Varieties

Intersection

Distributivity

Example

⊗ is Right-Exact

Induced B-Modules

Special Cases

1. Localization

2 Quotient

3 Polynomial (Exercise C)

Properties

Tensor Products

Construction

Basic Properties

Recent Posts

Archives

Categories

Meta

Pages