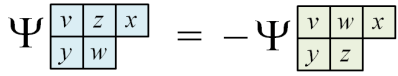Schreier-Sims Algorithm

Posted on June 12, 2018 by limsup

Introduction

Throughout this article, we let G be a subgroup of S_n generated by a subset A\subseteq S_n. We wish to consider the following questions.

  • Given A, how do we compute the order of G?
  • How do we determine if an element g\in S_n lies in G?
  • Assuming g\in G, how do we represent g as a product of elements of A and their inverses?

In general, the order of G is comparable to |S_n| = n! even for moderately-sized A so brute force is not a good solution.

We will answer the first two questions in this article. The third is trickier, but there is a nice algorithm by Minkwitz which works for most practical instances.

Application

We can represent the group of transformations of the Rubik’s cube as a subgroup of S_{48} generated by a set S of 6 permutations. The idea is to label each non-central unit square of each face by a number; a transformation of the Rubik’s cube then corresponds to a permutation of these 6 × 8 = 48 unit squares.

rubik_cube

[Image from official Rubik’s cube website.]

Our link above gives the exact order of the Rubik’s cube group (43252003274489856000), as computed by the open source algebra package GAP 4. How does it do that, without enumerating all the elements of the group? The answer will be given below.

blue-lin

Schreier-Sims Algorithm

To describe the Schreier-Sims algorithm, we use the following notations:

  • A\subseteq S_n is some subset represented in the computer’s memory;
  • G = \left< A\right> is a subgroup of S_n;
  • G acts on the set [n] := \{1, 2, \ldots, n\}.

Let us pick some random element k\in [n] and consider its orbit O_k under G. From the theory of group actions, we have

|O_k| = \frac{|G|}{|G_k|}

where G_k = \{g \in G: g(k) = k\} is the isotropy group of k. Now it is easy to compute the orbit of k: we start by setting the orbit to be the singleton {k}, then expand it by letting elements of A act on elements of this set. The process stops if we can’t add any more elements via this iteration. A more detailed algorithm will be provided later.

Thus, if we could effectively obtain a set of generators for G_k, our task would be complete since we could recursively apply the process to G_k. [Or so it seems: there’ll be a slight complication.]

For that, we pick a set U of representatives for the left cosets \{gG_k : g\in G\} as follows. For each j\in O_k, we pick some element g\in G which maps k\mapsto j, and for j = k we pick the identity. To facilitate this process, we use a data structure called a Schreier vector.

blue-lin

Schreier Vector for Computing Orbits

Warning: our description of the Schreier vector differs slightly from the usual implementation, since we admit the inverse of a generator.

Let us label the elements of the generating set A = \{g_1, g_2, \ldots, g_m\}.

  • Initialize an array (v[1], v[2], …, v[n]) of integers to -1.
  • Set v[k] := 0.
  • For each i = 1, 2, …, n:
    • If v[i] = -1 we ignore the next step.
    • For each r = 1, 2, …, m, we set g = gr:
      • set j := g(i); if v[j] = -1, then set v[j] = 2r-1;
      • set j := g-1(i): if v[j] = -1, then set v[j] = 2r.
  • Repeat the previous step until no more changes were made to v.

The idea is that v contains a “pointer” to an element of A (or its inverse) which brings it one step closer to k.

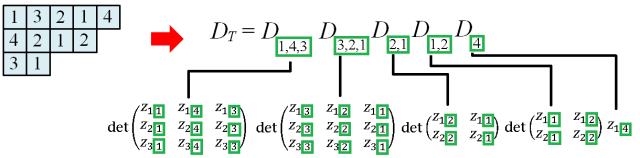
Example

Suppose we have elements

a = (1, 5, 3, 2)(4, 7, 9), \quad b = (1, 6, 7).

Labelling a = g_1 and b = g_2, we obtain the following Schreier vector for k=1:

schreier_vector_example

Thus the orbit of 1 is {1, 2, 3, 4, 5, 6, 7, 9}. To compute an element which maps 1 to, say, 9, the vector gives us ab^{-1}(1) = 9. Hence we can pick the following for U

U = \{e, a^{-1}, a^{-2}, a^{-1}b^{-1}, a, b, b^{-1}, ab^{-1}\}.

blue-lin

Key Lemma

Next, we define the map \phi : G\to U which takes g\in G to the unique u\in U such that gG_k = uG_k (i.e. u is the unique element of U satisfying u(k) = g(k)). Our main result is:

Schreier’s Lemma.

The subgroup G_k is generated by the following set

B := \{ \phi(au)^{-1} au : a\in A, u\in U\}.

Proof

First note that \phi(au)^{-1} au takes k to itself: indeed \phi(au) by definition takes k to au(k). Thus we see that each \phi(au)^{-1} au\in G_k as desired so \left<B\right>\le G_k.

Next, observe that B is precisely the set of all u'^{-1}au for u, u'\in U and a\in A which lies in G_k. Indeed for such an element, u’ must be the unique element of U which maps k to au(k) and so u' = \phi(au).

Now suppose h\in G_k; we write it as a product of elements of A and their inverses:

h = a_1^{\epsilon_1} a_2^{\epsilon_2} \ldots a_m^{\epsilon_m}, \quad \epsilon_i = \pm 1.

We will write

u_0^{-1}hu_m = (u_0^{-1} a_1^{\epsilon_1} u_1)\cdot (u_1^{-1} a_2^{\epsilon_2} u_2)\ldots (u_{m-1}^{-1} a_m^{\epsilon_m} u_m),

where u_0, u_1, \ldots, u_m\in U are elements to be recursively chosen. Specifically we start with u_m := e\in U, and for each u_{i+1}\in U we set u_i := \phi(a_{i+1}u_{i+1}). Note that each term in parentheses is an element of B\cup B^{-1}. Thus, the expression lies in G_k.

So we have u_0 = \phi(hu_m) = \phi(h). Since h\in G_k, this gives u_0=e as well so we have obtained h as a product of elements of B and their inverses. ♦

blue-lin

Example

Consider the subgroup G\le S_{8} generated by

a = (1, 5, 7)(2, 6, 8), \quad b = (1, 5)(3, 4, 8, 2).

If we pick k = 1, its orbit is O_k = \{1, 5, 7\}. For the coset representatives U, we take:

1 \mapsto g_1 = e, \quad 5 \mapsto g_5 = b, \quad 7\mapsto g_7 =a^{-1}.

Now the subgroup G_k is generated by the following 6 elements:

\begin{matrix}g_5^{-1}ag_1 = (2, 6, 4, 3)(5, 7), & g_7^{-1}ag_5 = (2, 3, 4, 6)(5, 7), & g_1^{-1}ag_7 = e, \\ g_5^{-1} b g_1 = e, &g_1^{-1}bg_5 = (2, 4)(3, 8),& g_7^{-1}bg_7 = (2, 6, 3, 4)(5, 7).\end{matrix}

Let H\le S_8 be the subgroup generated by these 6 elements; after removing the identity elements we are left with 4. Now if we pick k = 2 next, we obtain 5 representatives for the next U and thus, we obtain up to 20 generators for the stabilizer of {1, 2} in G.

Problem

The number of generators for the stabilizer groups seems to be ballooning: we started off with 2 examples, then expanded to 6 (but trimmed down to 4), then blew up to 20 after the second iteration.

Indeed, if we naively pick \{\phi(au)^{-1}au\} over all (a,u) \in A\times U, then the number of generator increases |U| = |O_k| times, while the order of the group decreases |O_k| times as well. Thus, at worst, the number of generators is comparable to the order of the group, which is unmanageable.

Thankfully, we have a way to pare down the number of generators.

blue-lin

Sims Filter

Sims Filter achieves the following.

Task.

Given a set A \subseteq S_n, there is an effective algorithm to replace A by some B\subseteq S_n satisfying \left<A\right> = \left<B\right> and

|B| \le \min\{|A|, \frac{n(n-1)}2\}.

Let us explain the filter now. For any non-identity permutation g\in S_n, let J(g) be the pair (i, j) with 1 \le i < j\le n such that g(a) = a for all 1\le a < i and g(i) = j.

sims_function

Now we will construct a set B such that \left<A\right> = \left<B\right> and the elements \pi\in B all have distinct J(\pi). It thus follows that |B| \le \frac{n(n-1)}2.

  1. Label A = \{g_1, g_2, \ldots, g_m\}.
  2. Prepare a table indexed by (i, j) for all 1\le i<j\le n. Initially this table is empty.
  3. For each g_k \in A, if g_k = e we drop it.
  4. Otherwise, consider J(g_k) = (i, j). If the table entry at (i, j) is empty, we fill g_k in. Otherwise, if the entry is h\in S_n, we replace g_k with g_k' := g_k^{-1}h and repeat step 3.
    • Note that this new group element takes i to i so if it is non-identity, we have J(g_k') = (i', j') with i' > i

After the whole process, the entries in the table give us the new set B. Clearly, we have |B| \le \min\{|A|, \frac{n(n-1)}2\}.

Example

As above, let us take A = {a, b} with

a = (1, 5, 7)(2, 6, 8), b = (1, 5)(3, 4, 8, 2) \in S_8.

First step: since J(a) = (1, 5) we fill the element a in the table at (1, 5).

Second step: we also have J(b) = (1, 5), so now we have to replace b with

b' := b^{-1}a = (2, 6, 4, 3)(5, 7).

Now we have J(b’) = (2, 6) so this is allowed.

blue-lin

Summary and Applications

In summary, we denote G^{(0)} = G and A^{(0)} = A.

  • For i = 1, 2, …
    • Pick a point k_i \in [n] not picked earlier.
    • Let G^{(i)} be the stabilizer group for k_i under the action of G^{(i-1)}. From A^{(i-1)}, we use Schreier’s lemma to obtain a generating set for G^{(i)}.
    • Use Sims filter to reduce this set to obtain A^{(i)} of at most \frac{n(n-1)}2 elements.
    • If A^{(i)} is empty, quit.

Thus k_1, k_2, \ldots, k_m \in [n] = \{1, 2, \ldots, n\} are distinct such that each of the groups

G = G^{(0)} \ge G^{(1)} \ge \ldots \ge G^{(m)} = 1, \\ G^{(i)} := \{g \in G : g(k_1) = k_1, \ldots, g(k_i) = k_i\}

has an explicit set of generators of at most \frac{n(n-1)}2 elements. Here are some applications of having this data.

1. Computing |G|.

It suffices to compute \frac{|G^{(i)}|}{|G^{(i+1)}|} for each i. Since G^{(i+1)} is the stabilizer group for the action of G^{(i)} on k_{i+1} we need to compute the size of the orbit G^{(i)}\cdot k_{i+1} for each i. Since we have a generating set for each G^{(i)}, this is easy.

2. Determining if a given g\in S_n lies in G.

To check if g\in G we first check whether g(k_1) lies in the orbit G\cdot k_1. If it weren’t, g\not\in G. Otherwise we pick some h\in G such that h(k_1) = g(k_1). Replacing g with h^{-1}g, we may thus assume that g(k_1) = k_1, and it follows that g\in G= G^{(0)} if and only if g\in G^{(1)}. Thus we can solve the problem inductively.

Generalizing, we can determine if H\le S_n is a subgroup of G\le S_n, when H and G are given by explicit sets of generators.

3. Checking if H\le S_n is a normal subgroup of G\le S_n.

Writing G = \left<A\right> and H = \left<B\right>, we claim that H is normal in G if and only if:

g\in A, h\in B \implies ghg^{-1} \in H.

First we fix g\in G. Since (ghg^{-1})(gh'g^{-1}) = ghh'g^{-1} and (ghg^{-1})^{-1} = gh^{-1}g^{-1}, we see that gHg^{-1} \subseteq H. But both groups are of the same finite cardinality so equality holds. Thus g^{-1}Hg = H as well. It follows that gHg^{-1} = H for all g\in G.

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Primality Tests III

Posted on June 6, 2018 by limsup

Solovay-Strassen Test

This is an enhancement of the Euler test. Be forewarned that it is in fact weaker than the Rabin-Miller test so it may not be of much practical interest. Nevertheless, it’s included here for completeness.

Recall that to perform the Euler test on an odd n, we pick a base a and check if a^{(n-1)/2} \equiv \pm 1 \pmod n.

To enhance this, we note that if p > 2 is prime, the value a^{\frac{p-1}2} modulo p tells us whether a is a square modulo p. We had written extensively on this before – in short, the Legendre symbol (\frac a p) := a^{\frac{p-1} 2} \mod p satisfies:

\left( \frac a p\right) = \begin{cases} +1, \quad &\text{if } a \text{ is a quadratic residue modulo } p\\ -1, \quad &\text{if } a \text{ is a non-quadratic residue modulo } p\\0, \quad &\text{if } a \text{ is divisible by } p\end{cases}

\left( \frac {-1} p\right) = \begin{cases} 1,\quad&\text{if } p\equiv 1 \pmod 4,\\ -1,\quad &\text{if }p \equiv -1\pmod 4.\end{cases}

\left( \frac 2 p\right) = \begin{cases} 1,\quad &\text{if } p\equiv 1, 7\pmod 8,\\ -1, \quad &\text{if } p \equiv 3, 5\pmod 8.\end{cases}

\left( \frac{ab} p\right) = \left( \frac a p\right) \left( \frac b p\right).

a \equiv b \pmod p \implies \left( \frac a p\right) = \left( \frac b p\right).

p, q \text{ odd prime} \implies \left( \frac q p\right) = (-1)^{\frac{p-1}2 \frac{q-1} 2}\left( \frac p q\right).

Observe that the second, fourth and fifth properties follow easily from the definition of the Legendre symbol. The last property, known as the quadratic reciprocity law, is highly non-trivial and is the seed of an extremely deep area of algebraic number theory, called class field theory. But that’s a story for another day.

Now, if we had another way to compute the Legendre symbol (\frac a p) and extend its definition to (\frac a n), we could compute a^{\frac {n-1}2} \mod n and compare the two.

blue-lin

Jacobi Symbol

Let us extend the Legendre symbol to the Jacobi symbol.

Definition.

Let a be any integer and n be an odd positive integer. Write

n = p_1^{r_1} p_2^{r_2} \ldots p_d^{r_d}

be its prime factorization. The Jacobi symbol is defined via:

\left(\frac a n\right) := \left(\frac a {p_1}\right)^{r_1} \left(\frac a {p_2}\right)^{r_2} \ldots \left(\frac a {p_d}\right)^{r_d}

where each term \left(\frac a {p_i}\right) is the Legendre symbol.

The Jacobi symbol inherits most properties of the Legendre symbol.

Exercise

Prove the following properties of the Jacobi symbol.

\left( \frac {-1} n\right) = \begin{cases} 1,\quad&\text{if } n\equiv 1 \pmod 4,\\ -1,\quad &\text{if }n \equiv -1\pmod 4.\end{cases}

\left( \frac 2 n\right) = \begin{cases} 1,\quad &\text{if } n\equiv 1, 7\pmod 8,\\ -1, \quad &\text{if } n \equiv 3, 5\pmod 8.\end{cases}

\left( \frac{ab} n\right) = \left( \frac a n\right) \left( \frac b n\right).

a \equiv b \pmod n \implies \left(\frac a n\right) = \left(\frac b n\right).

m, n \text{ odd positive} \implies \left( \frac n m\right) = (-1)^{\frac{m-1}2 \frac{n-1} 2}\left( \frac m n\right).

Proof

We will only prove the last property as an example. First note that when m and n are odd primes, the result is just the quadratic reciprocity theorem. Since we have (\frac a n)(\frac b n) = (\frac {ab} n) and (\frac a {mn}) = (\frac a m)(\frac a n) it suffices to define, for positive odd m and n,

D(m, n) = (-1)^{\frac {m-1}2\frac {n-1}2}

and prove D(mm', n) = D(m, n)D(m',n) and D(m, nn') = D(m,n) D(m,n'). The two claims are identical, so let’s just show the first, which is equivalent to:

\frac{mm' - 1}2 \frac{n-1}2 \equiv \frac {m-1}2 \frac{n-1}2 + \frac{m'-1}2 \frac{n-1}2 \pmod 2.

But this is obvious: the difference between the two sides is \frac{(m-1)(m'-1)}2 \frac{n-1}2 which is clearly even. ♦

blue-lin

Computing the Jacobi Symbol

We thus have a computationally feasible way to compute the Jacobi symbol recursively for extremely large integers. E.g. to compute (\frac {69}{133}) we repeatedly apply the above properties to obtain:

(\frac{33}{89}) = (\frac{89}{33}) = (\frac{23}{33}) = (\frac{33}{23}) = (\frac{10}{23}) = (\frac 2 {23})(\frac 5 {23}) = (\frac 5 {23}) = (\frac {23} 5) = (\frac 3 5) = (\frac 5 3) = (\frac 2 3) = -1.

In Python code, we have:

def jacobi(m, n):
   if m == 0:
      return 0

   if m == 1:
      return 1

   if m < 0:
      if (n%4 == 3):
         return -jacobi(-m, n)
      else:
         return +jacobi(-m, n)

   if (m >= n):
      return jacobi(m%n, n)

   if m % 2 == 0:
      if (n%8 == 3 or n%8 == 5):
         return -jacobi(m/2, n)
      else:
         return +jacobi(m/2, n)

   if m % 4 == 3 and n % 4 == 3:
      return -jacobi(n, m)
   else:
      return jacobi(n, m)

Now we can describe our main objective.

blue-lin

Description of Test

Solovay-Strassen Test.

Given an odd n and base a, compute the Jacobi symbol (\frac a n). Now check that

a^{\frac{n-1} 2} \equiv (\frac a n) \pmod n

and that both sides are non-zero.

Example

Let n = 10261 and a = 2. Immediately the Jacobi symbol gives (\frac a n) = -1. On the other hand, a^{\frac {n-1}2}\equiv 1 \pmod n. Thus even though n passes the Euler test for base 2, it fails the Solovay-Strassen test for the same base.

Notice that this also fails the Rabin-Miller test for the same base since

2^{(n-1)/4} \equiv 1985 \not\equiv \pm 1 \pmod n but 2^{(n-1)/2} \equiv 1 \pmod n.

In fact, the following is true in general.

Theorem.

If odd n passes the Rabin-Miller test to base a, then it also passes the Solovay-Strassen test to the same base.

For a proof of the result, see theorem 3 of this paper. This is why we said there’s not much practical application for this test.

blue-lin

 

Posted in Uncategorized | Tagged , , , , , , , | Leave a comment

Primality Tests II

Posted on June 5, 2018 by limsup

In this article, we discuss some ways of improving the basic Fermat test. Recall that for Fermat test, to test if n is prime, one picks a base a < n and checks if a^{n-1} \equiv 1 \pmod n. We also saw that this method would utterly fail when we throw a Carmichael number at it.

Euler Test

The basic enhancement is as follows.

Lemma.

If p is prime and m^2 \equiv  1 \pmod p, then m \equiv \pm 1 \pmod p.

The lemma is quite easy to prove. By the given condition m^2 - 1 = (m-1)(m+1) is a multiple of p and since p is prime either (m – 1) or (m + 1) is a multiple of p and the result follows.

In particular, if p is an odd prime and a is not divisible by p, then by Fermat’s theorem we have:

\left(a^{\frac{p-1} 2}\right)^2 = a^{p-1} \equiv 1 \pmod p \implies a^{\frac{p-1}2} \equiv \pm 1\pmod p.

In other words, to test if an odd n is prime, we pick a base a < n and check if a^{\frac{n-1}2}\equiv \pm 1\pmod n. If it is not, then n is not prime. This is called the Euler test with base a.

Note that the Euler test is necessarily stronger than the Fermat test since if a^{\frac{n-1}2} \equiv \pm 1\pmod n, then we must have a^{n-1}\equiv 1\pmod n.

Example 1

Consider n = 11305. We pick the smallest base a = 2. This gives us:

a^{\frac{n-1}2} = 2^{5652} \equiv 10641 \not\equiv \pm 1 \pmod {n}.

Notice that the Fermat with the same base would give a^{n-1} \equiv 10641^2 \equiv 1  \pmod n. Hence a pseudoprime can be picked up by the Euler test.

Example 2

Suppose we pick n = 10585 as before. We obtain:

2^{\frac{n-1}2} \equiv 3^{\frac{n-1}2} \equiv 1 \pmod n

so Euler test is not more effective than Fermat test in this case.

Example 3

Let’s pick the smallest Carmichael number n = 561. We have:

5^{\frac {n-1} 2} = 5^{280} \equiv 67 \pmod {561}

so there are Carmichael numbers which succumb to the Euler test.

In conclusion, the Euler test is strictly stronger than the Fermat test. Furthermore, it’s a little faster since we only need to compute a^{\frac {n-1} 2} \mod n instead of a^{n-1} \mod n.

blue-lin

Euler Pseudoprimes

As we saw above, even composite n can pass the Euler test for some bases.

Definition.

If n is odd composite and a\ne 1 is such that a^{\frac{n-1}2} \equiv 1 \pmod n, then we say n is an Euler pseudoprime to base a.

Thus from our above example, 10585 is an Euler pseudoprime to bases 2 and 3.

Clearly, if n is an Euler pseudoprime to base a, then it is also a pseudoprime to base a. However, as example 1 above shows, there are pseudoprimes which are not Euler pseudoprimes (for a fixed given base). As example 3 shows, some Carmichael numbers can fail the Euler test, which spells good news for us.

Unfortunately, not all Carmichael numbers can be identified composite by the Euler test. Specifically, there are odd composite n which is an Euler pseudoprime for all a which are coprime to n. Such numbers are known as absolute Euler pseudoprimes. It turns out Chernick’s construction for Carmichael numbers also gives us absolute Euler pseudoprimes.

Exercise

Suppose k is a positive integer such that 6k + 1, 12k + 1 and 18k + 1 are prime. Prove that n := (6k + 1)(12k + 1)(18k + 1) is an absolute Euler pseudoprime.

Thus, we are not quite out of the woods yet.

blue-lin

Rabin-Miller Test

As we noted above, if p is prime then whenever m^2\equiv 1\pmod p we have m \equiv \pm 1 \pmod p. This observation helps us to identify the pseudoprime n = 10585 in example 2.

Indeed, we have 2^{\frac {n-1}2} \equiv 1 \pmod  n. However, since \frac {n-1}2 is even, we can go one step further and check if 2^{\frac {n-1}4} \equiv \pm 1 \pmod n. In our case, we obtain 2^{\frac {n-1}4} \equiv 10294 \not\equiv \pm1 \pmod n and thus we see that n is composite.

This is the gist of the Rabin-Miller test. The idea is that if a^{(n-1)/2^k} \equiv 1 \pmod n and the exponent {\frac {n-1} {2^k}} is even, then we check whether

a^{(n-1)/2^{k+1}} \equiv \pm 1 \pmod n.

If it is not, n must be composite.

Rabin-Miller Test.

Suppose a\ne 1 is a given base and n is odd. Let 2^k be the highest power of 2 dividing n-1 and compute

r := a^{(n-1)/2^k} \mod n.

Perform the following for k-1 iterations.

  1. If r \equiv \pm 1 \pmod n, output PASS.
  2. Let r \leftarrow r^2 \mod n.
  3. If  r \equiv +1 \pmod n, output FAIL.
  4. Go back to step 1.

Example

If we set n = 10585 and a = 2 as above, then k = 3 and \frac{n-1} {2^k} = 1323. Thus we have r = 2^{1323} \mod n = 7958.

During the first iteration, we skip through step 1, set r\leftarrow r^2 \mod n = 10294. Thus we skip step 3 as well.

During the second iteration, we skip through step 1, set r\leftarrow r^2\mod n = 1. Thus step 3 says n fails the test.

blue-lin

Effectiveness of Rabin-Miller

Clearly the Rabin-Miller test is stronger than the Euler test, but just how much stronger is it? There are indeed composite numbers which pass the Rabin-Miller test for specific bases. These are called strong pseudoprimes.

Example

Suppose n = 8321 and a = 2. The highest power of 2 dividing n-1 is 27. Hence we have r = 2^{8320/128} \equiv 8192 \pmod n. The next iteration then gives r \equiv 8192^2 \equiv -1 \pmod n so n passes the Rabin-Miller test to base 2.

On the other hand, one easily checks that n fails the Fermat test for base 3 so it is composite.

Thankfully, we do not have the case of Carmichael numbers here.

Theorem.

If n is odd composite, it will fail the Rabin-Miller test for 75% of a within the range 1 < a < n.

Thus, for a given odd n we randomly pick 1 < a < n for about 20 trials. If n passes all trials, we report that it is most likely prime. Otherwise, if it fails even a single trial, then it is composite. Heuristically, one imagines that the probability of n being composite and passing all trials to be about (\frac 1 4)^{20} = 2^{-40}. In practice 75% is a gross underestimate since for most randomly chosen large n, the Rabin-Miller test will fail for >99% of the bases.

We have here a probabilistic primality testing method, in the sense that if n passes the test, it is overwhelmingly likely to be prime; on the other hand, any failure immediately implies n is composite.

Our confidence in the Rabin-Miller test is further enhanced by the following result.

Theorem (Miller).

Assuming the Generalized Riemann Hypothesis (GRH), if n passes the Rabin-Miller test for all 1 < a < 2(\log n)^2, then it is prime.

Miller noted that the multiplicative group (\mathbb Z/n\mathbb Z)^* is generated by elements bounded by 2(\log n)^2 and thus it suffices to check for all bases in that bound. The conjecture remains open to this day – if you can prove it, you stand to win a million dollars. We will not delve into this topic since the GRH is an extremely deep result. However, we do note that there is overwhelming computational evidence in support of the conjecture and in practice it is reasonable to run the Rabin-Miller test within the above specified bound.

blue-lin

Summary

The Rabin-Miller test is a highly efficient and reliable, albeit probabilistic, primality test. In general, we would like our primality tests to satisfy the following conditions.

  • Deterministic: it can tell with absolute certainty if n is prime.
  • Efficient: its runtime is polynomial in the length of n (i.e. O((log n)d) for some d.
  • Unconditional: it does not assume any open conjecture.

If we run, say, 20 iterations of Rabin-Miller we obtain a probabilistic efficient test, i.e. the second and third conditions are satisfied but not the first. Assuming the GRH, we could test for all bases less than 2(log n)2 and obtain a primality test satisfying the first and second conditions but not the third.

In addition there’s a primality test by Adleman, Pomerance and Rumely which is based on the elliptic curve group. This test is deterministic and unconditional, but its runtime complexity is slightly worse than polynomial time (in log n). Thus, it satisfies the first and third properties but not the second. We may describe this test in a later article.

For years, computer scientists wondered if there is a deterministic, polynomial-time and unconditional primality test. This was finally answered in the affirmative in 2002 by Agrawal, Kayal and Saxena who found a test which satisfied all three conditions. Unfortunately, despite being polynomial in the size of n, the algorithm can only be used on very modestly sized numbers when applied in practice, despite extensive optimization efforts by various people.

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Primality Tests I

Posted on June 4, 2018 by limsup

Description of Problem

The main problem we wish to discuss is as follows.

Question. Given n, how do we determine if  it is prime?

Prime numbers have opened up huge avenues in theoretical research – the renowned Riemann Hypothesis, for example, is really a statement about the distribution of primes. On the other hand, it was only in the late 70s that people have found applications for them in computer science. Specifically, the RSA asymmetric encryption system requires the software to quickly generate huge prime numbers of several hundred digits. Hence, primality testing is of huge practical importance as well – in fact, without fast primality testing algorithms, asymmetric encryption systems would be totally absent.

[ Current state-of-the-art asymmetric encryption systems include RSA, Diffie-Hellman and elliptic curve cryptography, all of which rely heavily on the ability to generate huge primes quickly, among other things. ]

Curiously, primality testing turns out to be a much simpler problem than the task of factoring, where one needs to factor a given large integer. The current best algorithm for  the latter task, general number field sieve, is extremely involved and requires an understanding of algebraic number theory. In contrast, most primality testing algorithms require only elementary number theory (except for the elliptic curve primality proving method, which I’ve yet to decide if I will cover).

Trial Division

One obvious way to test if a number is prime is trial division. Thus, given n, we iteratively test whether n is divisible by k, for all k\le [\sqrt n].

Why [\sqrt n]? Because if n is divisible by some k, it is also divisible by n/k. Thus we may assume one of the factors to be at most \sqrt n. For example, given 103, we quickly find that it is prime since it is not divisible by 2, 3, …, 10.

In fact, if n is composite, then it is divisible by some prime number less than \sqrt n. However, iterating through prime numbers is computationally difficult so one usually doesn’t bother with that. On the other hand, this gives us a quick way to mentally test if n is prime for n < 400, since we only need to test for possible factors 2, 3, 5, 7, 11, 13, 17, 19.

Trial division is impractical for large numbers, but don’t knock it! When you need to code a quick function to test if a 32-bit number is prime, trial division is the way to go.

blue-lin

Fermat Test

The primary observation comes from the following number-theoretic result:

Fermat’s (Little) Theorem.

If p is prime and a is an integer not divisible by p, then

a^{p-1} \equiv 1 \pmod p.

Thus the contrapositive statement says: if a is an integer not divisible by p and a^{p-1} \not\equiv 1 \pmod p, then p is not prime. This is called the Fermat test with base a. As example 2 below shows, it has its flaws.

Example 1

Consider the integer n = 15943. Picking a = 2, we have:

2^{15942} \equiv 5086 \not\equiv 1\pmod {15943}.

Hence n is composite.

Example 2

Consider the integer n = 10585. Fermat test then gives us

\begin{aligned} 2^{10584} &\equiv 1 \pmod {10585},\\ 3^{10584} &\equiv 1 \pmod {10585}, \\ 5^{10584} &\equiv 4235 \not\equiv 1 \pmod {10585}.\end{aligned}

Hence we see that n is composite. More importantly, this shows that Fermat test can fail for some bases.

Example 3

Let n = 10891. We see that:

2^{10890} \equiv 3^{10890} \equiv 5^{10890} \equiv 7^{10890} \equiv 1 \pmod {10891}.

Hence n appears to be prime. Indeed it is, as you can easily verify.

In summary, we have the following:

Fermat Test for n.

For various positive bases a<n, we check if a^{n-1} \equiv 1 \pmod n. If this fails for any a, we know that n is composite. Otherwise, n is most probably prime.

Exercise

Explain why, in the Fermat test, if we wish to test for all bases < A, it suffices to test for all prime bases < A.

blue-lin

Pseudoprimes

Example 2 above teaches us an important lesson: there are composite n and numbers a≠1 for which a^{n-1}\equiv 1 \pmod n.  Hence we have:

Definition.

If n is composite and a\ne 1 is such that a^{n-1} \equiv 1 \pmod n, then we say n is a pseudoprime with base a.

For a fixed base, pseudoprimes are rather rare. For example, the list of pseudoprimes with base 2 can be obtained on https://oeis.org/A001567 and there are only 22 of them below 10000 and 5597 of them below 10^9 (see http://oeis.org/A055550). Hence given a random huge composite number, chances are high that the first Fermat test will expose it. Put in another way, given a huge random number that passes the first Fermat test, chances are high it’s prime.

This seems to imply that if a large integer n passes (say) 30 Fermat tests, then it’s guaranteed to be prime.

Not really, for we have the following.

Definition.

If n is composite such that for all a coprime to n we have a^{n-1} \equiv 1 \pmod n, then we say n is a Carmichael number.

The smallest Carmichael number is 561 = 3 × 11 × 17.

While such numbers are rare, there are infinitely many of them. [ Fun fact: this conjecture remained open for a long time and was finally proven in 1994, by Alford, Granville and Pomerance. ] Note, however, that among the list of Carmichael numbers, each term seems to have a small prime factor; for instance, 561 is divisible by 3. So maybe we can combine Fermat test with trial division (by small primes) in order to weed out such cases?

No such luck, however. Chernick discovered in 1931 that if k is a positive integer such that 6k+1, 12k+1 and 18k+1 are all prime, then

n = (6k + 1)(12k + 1)(18k + 1)

is a Carmichael number. Now, it remains an open question whether there are infinitely many Carmichael numbers of this form, but in practice (from what we know of density of primes), it is quite easy to construct extremely large Carmichael numbers of this form. For instance, it takes only a few seconds for a Python script to give us the following 301-digit Carmichael number with three 100-digit prime factors:

3678977776333017616618572124346263612335718264220592681275
4323375966931049703503059541656515082721932203861403966236
1707445079748715571482964640305403211055421233151364221297
3982555078692571752850813633662021955795733617868645037712
1505333087445948159695018394505386803232557678106811464742
96899444481

Such a case would have no hope of getting picked up by a combination of Fermat test and trial division. But don’t give up yet, for the story is not over.

Exercises

Prove Chernick’s result. [This is one of those results which are easy to prove, but hard to obtain.]

Extend Chernick’s result to obtain a Carmichael number of >400 digits which has four prime divisors. What about five?

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Polynomials and Representations XXXIX

Posted on July 7, 2016 by limsup

Some Invariant Theory

We continue the previous discussion. Recall that for \mu = \overline\lambda we have a GL_n\mathbb{C}-equivariant map

\displaystyle \bigotimes_j \text{Alt}^{\mu_j} \mathbb{C}^n \to \bigotimes_i \text{Sym}^{\lambda_i} \mathbb{C}^n \subset\mathbb{C}[z_{i,j}]^{(\lambda_i)}, \quad e_T^\circ \mapsto D_T

which induces an isomorphism between the unique copies of V(\lambda) in both spaces. The kernel Q of this map is spanned by e_T^\circ - \sum_S e_S^\circ for various fillings T with shape \lambda and entries in [n].

E.g. suppose \lambda = (4, 3, 1) and n=5; then \mu = (3, 2, 2,1) and the map induces:

\displaystyle \text{Alt}^3 \mathbb{C}^5 \otimes \text{Alt}^2 \mathbb{C}^5 \otimes \text{Alt}^2 \mathbb{C}^5\otimes \mathbb{C}^5 \longrightarrow \mathbb{C}[z_{1,j}]^{(4)} \otimes \mathbb{C}[z_{2,j}]^{(3)}\otimes \mathbb{C}[z_{3,j}]^{(1)}, \ 1\le j \le 5,

with kernel Q. For the following filling T, we have the correspondence:

example_determinant_and_alt

Lemma. If \mu_j = \mu_{j+1} = \ldots = \mu_{j+m-1}, then the above map factors through

\displaystyle \text{Alt}^{\mu_j}\mathbb{C}^n \otimes \ldots \otimes \text{Alt}^{\mu_{j+m-1}}\mathbb{C}^n\longrightarrow \text{Sym}^m \left(\text{Alt}^{\mu_j} \mathbb{C}^n\right).

E.g. in our example above, the map factors through \text{Alt}^3 \mathbb{C}^5 \otimes \text{Sym}^2 \left(\text{Alt}^2 \mathbb{C}^5 \right)\otimes \mathbb{C}^5.

Proof

Indeed if \mu_j = \mu_{j+1}, then swapping columns j and j+1 of T gives us the same D_T. ♦

blue-lin

Now suppose 0\le a\le n and m\ge 0; pick \lambda = (m, \ldots, m) with length a. Now \mu comprises of m copies of a so by the above lemma, we have a map:

\displaystyle \text{Sym}^m \left(\text{Alt}^a \mathbb{C}^n\right) \longrightarrow \mathbb{C}[z_{1,j}]^{(m)} \otimes \ldots \otimes \mathbb{C}[z_{a,j}]^{(m)} \cong \mathbb{C}[z_{i,j}]^{(m,\ldots,m)}

where 1 \le i \le a and 1 \le j \le n. Taking the direct sum over all m we have:

\displaystyle \text{Sym}^* \left(\text{Alt}^a \mathbb{C}^n\right) := \bigoplus_{m\ge 0} \text{Sym}^m \left(\text{Alt}^a \mathbb{C}^n\right)\longrightarrow \bigoplus_{m\ge 0}\mathbb{C}[z_{i,j}]^{(m,\ldots,m)} \subset \mathbb{C}[z_{i,j}]

which is a homomorphism of GL_n\mathbb{C}-representations. Furthermore, \text{Sym}^* V for any vector space V has an algebra structure via \text{Sym}^m V \times \text{Sym}^n V \to \text{Sym}^{m+n}V. The above map clearly preserves multiplication since multiplying e_T^\circ e_{T'}^\circ and D_T D_{T'} both correspond to concatenation of T and T’. So it is also a homomorphism of \mathbb{C}-algebras.

Question. A basis of \text{Alt}^a\mathbb{C}^n is given by

\displaystyle e_{i_1, \ldots, i_a} := e_{i_1} \wedge \ldots \wedge e_{i_a}

for 1 \le i_1 < \ldots < i_a \le n. Hence \text{Sym}^*\left(\text{Alt}^a \mathbb{C}^n\right) \cong \mathbb{C}[e_{i_1,\ldots,i_a}], the ring of polynomials in n\choose a variables. What is the kernel P of the induced map:

\mathbb{C}[e_{i_1, \ldots, i_a}] \longrightarrow \mathbb{C}[z_{1,1}, \ldots, z_{a,n}]?

Answer

We have seen that for any 1 \le i_1 < \ldots < i_a \le n and 1 \le j_1 < \ldots < j_a \le n we have:

\displaystyle e_{i_1, \ldots, i_a} e_{j_1, \ldots, j_a} = \sum e_{i_1', \ldots, i_a'} e_{j_1', \ldots, j_k', j_{k+1},\ldots, j_a}

where we swap j_1, \ldots, j_k with various sets of k indices in i_1, \ldots, i_a while preserving the order to give (i_1', \ldots, i_a') and (j_1', \ldots, j_k'). Hence, P contains the ideal generated by all such quadratic relations.

On the other hand, any relation e_T = \sum_S e_S is a multiple of such a quadratic equation with a polynomial. This is clear by taking the two columns used in swapping; the remaining columns simply multiply the quadratic relation with a polynomial. Hence P is the ideal generated by these quadratic equations. ♦

Since the quotient of \mathbb{C}[e_{i_1, \ldots, i_a}] by P is a subring of \mathbb{C}[z_{i,j}], we have:

Corollary. The ideal generated by the above quadratic equations is prime.

blue-lin

Fundamental Theorems of Invariant Theory

Recall that g = (g_{i,j}) \in GL_n\mathbb{C} takes z_{i,j} \mapsto \sum_k z_{i,k} g_{k,j}, which is a left action; here 1\le i\le a, 1\le j\le n. We also let GL_a\mathbb{C} act on the right via:

\displaystyle g=(g_{i,j}) \in GL_a\mathbb{C} :z_{i,j} \mapsto \sum_k g_{i,k}z_{k,j}

so that \mathbb{C}[z_{i,j}] becomes a (GL_n\mathbb{C}, GL_a\mathbb{C})-bimodule. A basic problem in invariant theory is to describe the ring \mathbb{C}[z_{i,j}]^{SL_a\mathbb{C}} comprising of all f such that g\cdot f = f for all g\in SL_a\mathbb{C}.

Theorem. The ring \mathbb{C}[z_{i,j}]^{SL_a\mathbb{C}} is the image of:

\displaystyle \mathbb{C}[D_{i_1, \ldots, i_a}] \cong \mathbb{C}[e_{i_1, \ldots, i_a}]/P \hookrightarrow \mathbb{C}[z_{i,j}]

where (i_1, \ldots, i_a) runs over all 1 \le i_1 < \ldots < i_a \le n.

In other words, we have:

  • First Fundamental Theorem : the ring of SL_a\mathbb{C}-invariants in \mathbb{C}[z_{i,j}] is generated by \{D_{i_1, \ldots, i_a}: 1 \le i_1 < \ldots < i_a \le n\}.
  • Second Fundamental Theorem : the relations satisfied by these polynomials are generated by the above quadratic relations.

blue-lin

Proof of Fundamental Theorems

Note that g takes D_{i_1, \ldots, i_a} to:

\displaystyle \det{\small \begin{pmatrix} z_{1, i_1} & z_{1, i_2} & \ldots & z_{1, i_a} \\ z_{2, i_1} & z_{2, i_2} & \ldots & z_{2, i_a} \\ \vdots & \vdots & \ddots & \vdots \\ z_{a, i_1} & z_{a, i_2} & \ldots & z_{a, i_a}\end{pmatrix}} \mapsto \det {\small \begin{pmatrix}\sum_{j_1} g_{1,j_1} z_{j_1, i_1} & \ldots & \sum_{j_a} g_{1,j_a} z_{j_a, i_a} \\ \sum_{j_1} g_{2,j_1} z_{j_1, i_1} & \ldots & \sum_{j_a} g_{2,j_a} z_{j_a, i_a} \\ \vdots & \ddots & \vdots \\ \sum_{j_1} g_{a,j_1} z_{j_1, i_1} & \ldots & \sum_{j_a} g_{a,j_a} z_{j_a, i_a} \end{pmatrix}} = \det(g) D_{i_1, \ldots, i_a}

which is D_{i_1, \ldots, i_a} if g \in SL_a\mathbb{C}. Hence we have \mathbb{C}[D_{i_1, \ldots, i_a}] \subseteq \mathbb{C}[z_{i,j}]^{SL_a\mathbb{C}}. To prove equality, we show that their dimensions in degree d agree. By the previous article, the degree-d component of \mathbb{C}[e_{i_1, \ldots, i_a}]/P has a basis indexed by SSYT of type \lambda = (\frac d a, \ldots, \frac d a) and entries in [n]; if d is not a multiple of a, the component is 0.

Next we check the degree-d component of \mathbb{C}[z_{i,j}]^{SL_a\mathbb{C} }. As GL_a\mathbb{C}-representations, we have

\displaystyle \mathbb{C}[z_{i,j}] \cong \text{Sym}^*\left( (\mathbb{C}^a)^{\oplus n}\right)

where GL_a\mathbb{C} acts on \mathbb{C}^a canonically. Taking the degree-d component, once again this component is 0 if d is not a multiple of a. If a|d, it is the direct sum of \text{Sym}^{d_1} \mathbb{C}^a \otimes \ldots \otimes \text{Sym}^{d_n}\mathbb{C}^a over all d_1 + \ldots + d_n = \frac d a. The \psi of this submodule is h_{\lambda'} = \sum_{\mu'\vdash \frac d a} K_{\mu'\lambda'} s_{\mu'} where \lambda' is the sequence (d_1, \ldots, d_n). Hence

\displaystyle \text{Sym}^{d_1} \mathbb{C}^a \otimes \ldots \otimes \text{Sym}^{d_n}\mathbb{C}^a \cong \bigoplus_{\mu'\vdash \frac d a} V(\mu')^{\oplus K_{\mu'\lambda'}}.

Fix \mu' and sum over all (d_1, \ldots, d_n); we see that the number of copies of V(\mu') is the number of SSYT with shape \mu' and entries in [n]. The key observation is that each V(\mu') is an SL_a\mathbb{C}-irrep.

  • Indeed, \mathbb{C}^* \subset GL_a\mathbb{C} acts as a constant scalar on the whole of V(\mu') since \psi_{V(\mu')} = s_{\mu'} is homogeneous. Hence any SL_a\mathbb{C}-invariant subspace of V(\mu') is also GL_a\mathbb{C}-invariant.

Hence V(\mu')^{SL_a\mathbb{C}} is either the whole space or 0. From the proposition here, it is the whole space if and only if \mu' = (\frac d a, \ldots, \frac d a) with a terms (which corresponds to \det^{d/a}). Hence, the required dimension is the number of SSYT with shape (\frac d a, \ldots) and entries in [n]. ♦

blue-lin

Posted in Uncategorized | Tagged , , , , , | Leave a comment

Polynomials and Representations XXXVIII

Posted on July 4, 2016 by limsup

Determinant Modules

We will describe another construction for the Schur module.

Introduce variables z_{i,j} for i\ge 1, j\ge 1. For each sequence i_1, \ldots, i_p\ge 1 we define the following polynomials in z_{i,j}:

D_{i_1, \ldots, i_p} := \det{\small \begin{pmatrix} z_{1, i_1} & z_{1, i_2} & \ldots & z_{1, i_p} \\ z_{2, i_1} & z_{2, i_2} & \ldots & z_{2, i_p} \\ \vdots & \vdots & \ddots & \vdots \\ z_{p, i_1} & z_{p, i_2} & \ldots & z_{p, i_p}\end{pmatrix}}.

Now given a filling T of shape λ, we define:

D_T := D_{\text{col}(T, 1)} D_{\text{col}(T, 2)} \ldots

where \text{col}(T, i) is the sequence of entries from the i-th column of T. E.g.

determinant_products_and_filling

Let \mathbb{C}[z_{i,j}] be the ring of polynomials in z_{ij} with complex coefficients. Since we usually take entries of T from [n], we only need to consider the subring \mathbb{C}[z_{i,1}, \ldots, z_{i,n}].

blue-lin

Let \mu = \overline \lambda. Recall from earlier that any non-zero GL_n\mathbb{C}-equivariant map

\displaystyle \bigotimes_j \left(\text{Alt}^{\mu_j} \mathbb{C}^n\right) \longrightarrow \bigotimes_i \left(\text{Sym}^{\lambda_i} \mathbb{C}^n \right)

must induce an isomorphism between the unique copies of V(\lambda) in the source and target spaces. Given any filling T of shape \lambda, we let e^\circ_T be the element of \otimes_j \text{Alt}^{\mu_j} \mathbb{C}^n obtained by replacing each entry k in T by e_k, then taking the wedge of elements in each column, followed by the tensor product across columns:

basis_element_of_alt_tensor_module

Note that the image of e^\circ_T in F(V) is precisely e_T as defined in the last article.

Definition. We take the map

\displaystyle \bigotimes_j \left(\text{Alt}^{\mu_j} \mathbb{C}^n\right) \longrightarrow \bigotimes_i \left(\text{Sym}^{\lambda_i} \mathbb{C}^n \right), \quad e_T^\circ \mapsto D_T

where z_{i,j} belongs to component \text{Sym}^{\lambda_i}.

E.g. in our example above, D_T is homogeneous in z_{1,j} of degree 5, z_{2,j} of degree 4 and z_{3,j} of degree 3. We let g \in GL_n\mathbb{C} act on \mathbb{C}[z_{i,j}] via:

g = (g_{i,j}) : z_{i,j} \mapsto \sum_k z_{i,k}g_{k,j}.

Thus if we fix i and consider the variables \mathbf z_i := \{z_{i,j}\}_j as a row vector, then g: \mathbf z_i \mapsto \mathbf z_i g^t. From another point of view, if we take z_{i,1}, z_{i,2},\ldots as a basis, then the action is represented by matrix g since it takes the standard basis to the column vectors of g.

Proposition. The map is GL_n\mathbb{C}-equivariant.

Proof

The element g = (g_{i,j}) takes e_i \mapsto \sum_j g_{j,i} e_j by taking the column vectors of g; so

\displaystyle e_T \mapsto \sum_{j_1, \ldots, j_d} g_{j_1, i_1} g_{j_2, i_2} \ldots g_{j_d, i_d} e_{T'}

where T’ is the filling obtained from T by replacing its entries i_1, \ldots, i_d with j_1, \ldots, j_d correspondingly.

On the other hand, the determinant D_{i_1, \ldots, i_p} gets mapped to:

\det{\small \begin{pmatrix} z_{1, i_1} & z_{1, i_2} & \ldots & z_{1, i_p} \\ z_{2, i_1} & z_{2, i_2} & \ldots & z_{2, i_p} \\ \vdots & \vdots & \ddots & \vdots \\ z_{p, i_1} & z_{p, i_2} & \ldots & z_{p, i_p}\end{pmatrix}} \mapsto \det{\small \begin{pmatrix} \sum_{j_1} z_{1,j_1} g_{j_1, i_1} & \ldots & \sum_{j_p} z_{1, j_p}g_{j_p i_p}\\ \sum_{j_1}z_{2, j_1} g_{j_1, i_1} & \ldots & \sum_{j_p} z_{2, j_p}g_{j_p, i_p}  \\ \vdots & \ddots & \vdots \\ \sum_{j_1} z_{p, j_1} g_{j_1, i_1} & \ldots & \sum_{j_p} z_{p, j_p} g_{j_p, i_p} \end{pmatrix}}

which is \sum_{j_1, \ldots, j_d} g_{j_1, i_1} \ldots g_{j_d, i_d} D_{T'}. ♦

blue-lin

Since \otimes_j \text{Alt}^{\mu_j} \mathbb{C}^n contains exactly one copy of V(\lambda), it has a unique GL_n\mathbb{C}-submodule Q such that the quotient is isomorphic to V(\lambda). The resulting quotient is thus identical to the Schur module F(V), and the above map factors through

F(V) \to \otimes_i \text{Sym}^{\lambda_i} \mathbb{C}^n, \quad e_T \mapsto D_T.

Now we can apply results from the last article:

Corollary 1. The polynomials D_T satisfy the following:

  • D_T = 0 if T has two identical entries in the same column.
  • D_T + D_{T'} = 0 if T’ is obtained from T by swapping two entries in the same column.
  • D_T = \sum_S D_S, where S takes the set of all fillings obtained from T by swapping a fixed set of k entries in column j’ with arbitrary sets of k entries in column j (for fixed j < j’) while preserving the order.

Proof

Indeed, the above hold when we replace D_T by e_T. Now apply the above linear map. ♦

Corollary 2. The set of D_T, for all SSYT T with shape λ and entries in [n], is linearly independent over \mathbb{C}.

Proof

Indeed, the set of these e_T is linearly independent over \mathbb{C} and the above map is injective. ♦

Example 1.

Consider any bijective filling T for \lambda = (2, 1). Writing out the third relation in corollary 1 gives:

\left[\det\begin{pmatrix} a & c \\ b & d\end{pmatrix}\right] x = \left[\det\begin{pmatrix} x & c \\ y & d\end{pmatrix}\right] a + \left[ \det\begin{pmatrix} a & x \\ b & y\end{pmatrix}\right] c.

More generally, if \lambda satisfies \lambda_j = 2 and \lambda_{j'} = 1, the corresponding third relation is obtained by multiplying the above by a polynomial on both sides.

Example 2: Sylvester’s Identity

Take the 2 \times n SYT by writing 1,\ldots, n in the left column and n+1, \ldots, 2n in the right. Now D_T = D_{1,\ldots, n}D_{n+1, \ldots, 2n} is the product:

\det \overbrace{\begin{pmatrix} z_{1,1} & z_{1,2} & \ldots & z_{1,n} \\ z_{2,1} & z_{2,2} &\ldots & z_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ z_{n,1} & z_{n,2} & \ldots & z_{n,n} \end{pmatrix}}^M \det \overbrace{\begin{pmatrix} z_{1,n+1} & z_{1,n+2} & \ldots & z_{1,2n} \\ z_{2,n+1} & z_{2,n+2} &\ldots & z_{2,2n} \\ \vdots & \vdots & \ddots & \vdots \\ z_{n,n+1} & z_{n,n+2} & \ldots & z_{n,2n} \end{pmatrix}}^N.

In the sum D_T = \sum_S D_S, each summand is of the form D_S= \det M' \det N', where matrices M’, N’ are obtained from M, N respectively by swapping a fixed set of k columns in N with arbitrary sets of k columns in M while preserving the column order. E.g. for n=3 and k=2, picking the first two columns of N gives:

\begin{aligned} \det ( M_1 | M_2 | M_3) \det(N_1 | N_2| N_3) &= \det(N_1 | N_2 | M_3) \det(M_1 | M_2 | N_3) \\ +\det(N_1 | M_2 | N_2) \det(M_1 | M_3 | N_3) &+ \det(M_1 | N_1 | N_2) \det(M_2 | M_3 | N_3).\end{aligned}

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Polynomials and Representations XXXVII

Posted on July 1, 2016 by limsup

Notations and Recollections

For a partition \lambda\vdash d, one takes its Young diagram comprising of boxes. A filling is given by a function T:\lambda \to [m] for some positive integer m. When m=d, we will require the filling to be bijective, i.e. T contains {1,…,d} and each element occurs exactly once.

If w\in S_m and T:\lambda \to [m] is a filling, then w(T) = w\circ T is obtained by replacing each i in the filling with w(i). For a filling T, the corresponding row (resp. column) tabloid is denoted by {T} (resp. [T]).

Recall from an earlier discussion that we can express the S_d-irrep V_\lambda as a quotient of \mathbb{C}[S_d]b_{T_0} from the surjection:

\mathbb{C}[S_d] b_{T_0} \to \mathbb{C}[S_d] b_{T_0} a_{T_0}, \quad v \mapsto v a_{T_0}.

Here T_0 is any fixed bijective filling \lambda \to [d].

Concretely, a C-basis for \mathbb{C}[S_d]b_{T_0} is given by column tabloids [T] and the quotient is given by relations: [T] = \sum_{T'} [T'] where T’ runs through all column tabloids obtained from T as follows:

  • fix columns j < j’ and a set B of k boxes in column j’ of T; then T’ is obtained by switching B with a set of k boxes in column j of T, while preserving the order. E.g.

modulo_relations_for_specht

blue-lin

For Representations of GLn

From the previous article we have V(\lambda) = V^{\otimes d} \otimes_{\mathbb{C}[S_d]} V_\lambda, where V_\lambda is the quotient of the space of column tabloids described above. We let V^{\times \lambda} be the set of all functions \lambda \to V, i.e. the set of all fillings of λ with elements of V. We define the map:

\Psi : V^{\times\lambda} \to V^{\otimes d}\otimes_{\mathbb{C}[S_d]} V_\lambda, \quad (v_s)_{s\in\lambda} \mapsto \overbrace{\left[v_{T^{-1}(1)} \otimes \ldots \otimes v_{T^{-1}(d)}\right]}^{\in V^{\otimes d}} \otimes [T]

for any bijective filling T:\lambda \to [d]. This is independent of the T we pick; indeed if we replace T by w(T) = w\circ T  for w\in S_d, the resulting RHS would be:

\begin{aligned}\left[v_{T^{-1}w^{-1}(1)} \otimes \ldots \otimes v_{T^{-1}w^{-1}(d)}\right] \otimes [w(T)] &= \left[v_{T^{-1}w^{-1}(1)}\otimes \ldots \otimes v_{T^{-1} w^{-1}(d)}\right]w \otimes [T]\\ &= \left[v_{T^{-1}(1)} \otimes \ldots \otimes v_{T^{-1}(d)}\right] \otimes [T]\end{aligned}

where the first equality holds since the outer tensor product is over \mathbb{C}[S_d] and the second equality follows from our definition (v_1' \otimes \ldots \otimes v_d')w = v_{w(1)}' \otimes \ldots \otimes v_{w(d)}'. Hence \Psi is well-defined. It satisfies the following three properties.

Property C1. \Psi is multilinear in each component V.

In other words, if we fix s\in \lambda and consider \Psi as a function on V in component s of V^{\times\lambda}, then the resulting map is C-linear. E.g. if w'' = 2w + 3w', then:

c1_multilinear

This is clear.

Property C2. Suppose (v_s), (v'_s)\in V^{\times\lambda} are identical except v'_s = v_t and v'_t = v_s, where s,t\in \lambda are in the same column. Then \Psi((v'_s)) = -\Psi((v_s)).

c2_alternating

Proof

Let w\in S_d be the transposition swapping s and t. Then w([T]) = -[T] by alternating property of the column tabloid and w^2 = e. Thus:

\begin{aligned}\left[v'_{T^{-1}(1)} \otimes \ldots \otimes v'_{T^{-1}(d)}\right] \otimes [T] &= \left[ v_{T^{-1}w^{-1}(1)} \otimes \ldots \otimes v_{T^{-1}w^{-1}(d)}\right] \otimes -w([T])\\ &= -\left[v_{T^{-1}(1)} \otimes\ldots \otimes v_{T^{-1}(d)}\right]\otimes [T]. \end{aligned} ♦

Finally, we have:

Property C3. Let (v_s)\in V^{\times\lambda}. Fix two columns j<j' in the Young diagram for λ, and a set B of k boxes in column j’. As A runs through all sets  of k boxes in column j, let (v_s^A) \in V^{\times\lambda} be obtained by swapping entries in A with entries in B while preserving the order. Then:

\displaystyle \Psi((v_s)) = \sum_{|A| = |B|} \Psi((v_s^A)).

E.g. for any u,v,w,x,y,z\in V we have:

c3_column_swaps

Proof

Fix a bijective filling T:\lambda \to [d]. Then:

\begin{aligned}\Psi((v_s^A)) &= \left[v_{T^{-1}(1)}^A \otimes \ldots \otimes v_{T^{-1}(d)}^A\right] \otimes [T ]\\ &= \left[v_{T^{-1}w^{-1}(1)} \otimes \ldots \otimes v_{T^{-1}w^{-1}(d)}\right] \otimes [T] \\ &= \left[v_{T^{-1}(1)} \otimes \ldots \otimes v_{T^{-1}(d)}\right] \otimes w([T])\end{aligned}

where w\in S_d swaps the entries in A with those in B while preserving the order (note that w^2 =e). But the sum of all such w([T]) vanishes in V_\lambda. Hence \sum_A \Psi((v_s^A)) = 0. ♦

blue-lin

Universality

Definition. Let V, W be complex vector spaces. A map \Psi : V^{\times \lambda} \to W is said to be λ-alternating if properties C1, C2 and C3 hold.

The universal λ-alternating space (or the Schur module) for V is a pair (F(V), \Phi_V) where

  • F(V) is a complex vector space;
  • \Phi_V : V^{\times\lambda} \to F(V) is a λ-alternating map,

satisfying the following universal property: for any λ-alternating map \Psi : V^{\times\lambda} \to W to a complex vector space W, there is a unique linear map \alpha : F(V) \to W such that \alpha\circ \Phi_V = \Psi.

F(V) is not hard to construct: the universal space which satisfies C1 and C2 is the alternating space:

\displaystyle \left(\text{Alt}^{\mu_1} V\right) \otimes \ldots \otimes \left(\text{Alt}^{\mu_e}V\right), \quad \mu := \overline\lambda.

So the desired F(V) is obtained by taking the quotient of this space with all relations obtained by swapping a fixed set B of coordinates in \text{Alt}^{j'} with a set A of coordinates in \text{Alt}^j, and letting A vary over all |A| = |B|. E.g. the relation corresponding to our above example for C3 is:

\begin{aligned} &\left[ (u\wedge x\wedge z) \otimes (v\wedge y) \otimes w\right] -\left[ (u\wedge y\wedge z) \otimes (u\wedge x) \otimes w\right] \\ - &\left[ (v\wedge x\wedge y)\otimes (u\wedge z)\otimes w\right] - \left[ (u\wedge x\wedge w) \otimes (v\wedge z) \otimes w\right]\end{aligned}

over all u,v,w,x,y,z\in V.

By universality, the λ-alternating map \Psi: V^{\times\lambda} \to V^{\otimes d} \otimes_{\mathbb{C}[S_d]} V_\lambda thus induces a linear:

\alpha: F(V) \longrightarrow V^{\otimes d} \otimes_{\mathbb{C}[S_d]} V_\lambda.

You can probably guess what’s coming next.

Main Theorem. The above \alpha is an isomorphism.

blue-lin

Proof of Main Theorem

First observe that \alpha is surjective by the explicit construction of F(V) so it remains to show injectivity via dim(LHS) ≤ dim(RHS).

Now V^{\otimes d}\otimes_{\mathbb{C}[S_d]}V_\lambda \cong V(\lambda), and we saw earlier that its dimension is the number of SSYT with shape λ and entries in [n].

On the other hand, let e_1, \ldots, e_n be the standard basis of V= \mathbb{C}^n. If T is any filling with shape λ and entries in [n], we let e_T be the element of F(V) obtained by replacing each i in T by e_i \in V; then running through the map \Phi_V: V^{\times \lambda} \to F(V).

basis_element_of_schur_module

Claim. The set of e_T generates F(V), where T runs through all SSYT with shape λ and entries in [n].

Proof

Note that the set of e_T, as T runs through all fillings with shape λ and entries in [n], generates F(V).

Let us order the set of all fillings of T as follows: T’ > T if, in the rightmost column j where T’ and T differ, at the lowest (i,j) in which T_{ij}' \ne T_{ij}, we have T_{ij}' > T_{ij}.

comparison_of_two_fillings

This gives a total ordering on the set of fillings. We claim that if T is a filling which is not an SSYT, then e_T is a linear combination of e_S for S > T.

  • If two entries in a column of T are equal, then e_T = 0 by definition.
  • If a column j and row i of T satisfy T_{i,j} > T_{i+1,j}, assume j is the rightmost column for which this happens, and in that column, i is as large as possible. Swapping entries (i,j) and (i+1, j) of T gives us T’ > T and e_T = -e_{T'}.
  • Now suppose all the columns are strictly ascending. Assume we have T_{i,j} > T_{i, j+1}, where j is the largest for which this happens, and T_{k,j} \le T_{k,j+1}, for k=1,\ldots, i-1. Swapping the topmost i entries of column j+1, with various  i entries of column j, all the resulting fillings are strictly greater than T. Hence e_T = -\sum_S e_S, where each S > T.

Thus, if T is not an SSYT we can replace e_T with a linear combination of e_S where S > T. Since there are finitely many fillings T (with entries in [n]), this process must eventually terminate so each e_T can be written as a linear sum of e_S for SSYT S. ♦

Thus \dim F(V) ≤ number of SSYT with shape λ and entries in [n], and the proof for the main theorem is complete. From our proof, we have also obtained:

Lemma. The set of \{e_T\} forms a basis for F(V), where T runs through the set of all SSYT with shape λ and entries in [n].

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Polynomials and Representations XXXVI

Posted on June 29, 2016 by limsup

V(λ) as Schur Functor

Again, we will denote V := \mathbb{C}^n throughout this article. In the previous article, we saw that the Schur-Weyl duality can be described as a functor:

  • given a \mathbb{C}[S_d]-module M, the corresponding GL_n\mathbb{C}-module is set as \text{Hom}_{S_d}(M, V^{\otimes d}).

Definition. The construction

F_M(V) := \text{Hom}_{S_d}(M, V^{\otimes d})

is functorial in V and is called the Schur functor when M is fixed.

Here, functoriality means that any linear map V\to W induces a linear F_M(V) \to F_M(W).

For example, when M = \mathbb{C}[S_d], the functor F_M is the identity functor. By Schur-Weyl duality, when M is irreducible as an S_d-module, the resulting F_M(V) is either 0 or irreducible. We will see the Schur functor cropping up in two other instances.

blue-lin

Following the reasoning as in S_d-modules, we have for partitions \lambda\vdash d and \mu := \overline\lambda,

\begin{aligned}\text{Sym}^\lambda V &:= \bigotimes_i \text{Sym}^{\lambda_i} V = V(\lambda) \oplus\left( \bigoplus_{\nu\trianglerighteq \lambda, \nu\ne\lambda} V(\nu)^{\oplus K_{\nu\lambda}}\right),\\ \text{Alt}^{\mu} V &:= \bigotimes_j \text{Alt}^{\mu_j}V = V(\lambda) \oplus \left(\bigoplus_{\nu\trianglelefteq \lambda, \nu\ne\lambda} V(\nu)^{\oplus K_{\overline\nu\mu}} \right).\end{aligned}

Since the only common irrep between the two representations is V(\lambda), any non-zero G-equivariant f: \text{Sym}^\lambda V\to \text{Alt}^\mu V must induce an isomorphism between those two components. We proceed to construct such a map.

For illustration, take \lambda = (3, 1) and pick the following filling:

young_diagram_label_1_to_n_v2

To construct the map, we will take \text{Sym}^d V and \text{Alt}^d as subspaces of V^{\otimes d}. Thus:

\begin{aligned}\text{Sym}^d V \subseteq V^{\otimes d},\quad& v_1 \ldots v_d \mapsto \sum_{w\in S_d} v_{w(1)} \otimes \ldots \otimes v_{w(d)},\\ \text{Alt}^d V\subseteq V^{\otimes d},\quad &v_1 \wedge \ldots \wedge v_d \mapsto \sum_{w\in S_d} \chi(w) v_{w(1)} \otimes \ldots \otimes v_{w(d)},\\ V^{\otimes d}\twoheadrightarrow \text{Sym}^d V, \quad &v_1 \otimes \ldots\otimes v_d \mapsto v_1 \ldots v_d, \\ V^{\otimes d} \twoheadrightarrow \text{Alt}^d V, \quad &v_1 \otimes \ldots \otimes v_d \mapsto v_1 \wedge \ldots \wedge v_d.\end{aligned}

Let us map \text{Sym}^\lambda V \to V^{\otimes 4} according to the above filling, i.e. \text{Sym}^3 V goes into components 1, 4, 2 of V^{\otimes 4} while V goes into component 3. Similarly, we map V^{\otimes 4} \to \text{Alt}^\mu V by mapping components 1, 3 to \text{Alt}^2 V, components 4 and 2 to the other two copies of V. In diagram, we have:

schur_functor_vector_space_constr

This construction is clearly functorial in V. Hence, if f:V\to W is a linear map of vector spaces, then this induces a linear map f(\lambda) : V(\lambda) \to W(\lambda).

blue-lin

Young Symmetrizer Revisited

Another means of defining the Schur functor is by the Young symmetrizer. Here we shall let GL_n\mathbb{C} act on V^{\otimes d} on the left and S_d act on it on the right via:

w\in S_d \implies(v_1 \otimes \ldots \otimes v_d)w := v_{w(1)} \otimes \ldots \otimes v_{w(d)}.

Now given any (left) \mathbb{C}[S_d]-module M, consider:

V(M) := V^{\otimes d} \otimes_{\mathbb{C}[G]} M,

a left GL_n\mathbb{C}-module. We shall prove that V(M) corresponds to the Schur-Weyl duality, i.e. M = V_\lambda \implies V(M) \cong V(\lambda). Once again, by additivity, we only need to consider the case M = \mathbb{C}[X_\lambda]. This gives M \cong \mathbb{C}[G]a_T where T is any filling of shape λ and thus:

V(M) = V^{\otimes d} \otimes_{\mathbb{C}[G]} \mathbb{C}[G]a_T \cong V^{\otimes d}a_T.

From here, it is clear that V(M) \cong \text{Sym}^\lambda V and so V\mapsto V(M) is yet another expression of the Schur functor.

Recall that the irreducible S_d-module V_\lambda can be written as \mathbb{C}[S_d]c_T where c_T is the Young symmetrizer for a fixed filling of shape λ. Hence, the irrep V(\lambda) can be written as:

V^{\otimes d} \otimes_{\mathbb{C}[G]} V_\lambda \cong V^{\otimes d}\otimes_{\mathbb{C}[G]} \mathbb{C}[G]c_T \cong V^{\otimes d}c_T.

blue-lin

Example: d=3

For d=3, and \lambda = (2,1), let us take the Young symmetrizer:

c_T = a_T b_T = (e + (1,2))(e - (1,3)) = e + (1,2) - (1,3) - (1,3,2).

If e_1, \ldots, e_n is the standard basis for V= \mathbb{C}^n, then V^{\otimes d}c_T is spanned by elements of the form:

\alpha_{i,j,k} := e_i \otimes e_j \otimes e_k + e_j \otimes e_i \otimes e_k - e_k \otimes e_j \otimes e_i - e_k \otimes e_i \otimes e_j, \ 1 \le i, j, k\le n.

These satisfy the following:

\alpha_{j,i,k} = \alpha_{i,j,k},\quad \alpha_{i,j,k} + \alpha_{j,k,i} + \alpha_{k,i,j} = 0.

By the first relation, we only include those \alpha_{i,j,k} with i \le j. By the second relation, we may further restrict to the case i<k since if i=k we have \alpha_{i,j,k} = 0 and if k <i\le j we replace \alpha_{i,j,k} = \alpha_{k,j,i}+ \alpha_{k,i,j}. We claim that the resulting spanning set \{\alpha_{i,j,k} : i\le j, i<k\} forms a basis. Indeed the number of such triplets (i, j, k) is:

d = \sum_{i=1}^n (n-i+1)(n-i) = \frac{n(n+1)(n-1)}3.

On the other hand, we know that V^{\otimes 3} has one copy of \text{Sym}^3, one copy of \text{Alt}^3 and two copies of V(\lambda) so

2\dim V = n^3 - \frac{(n+2)(n+1)n}6 - \frac{n(n-1)(n-2)}6 =\frac{2n(n+1)(n-1)}3.

Thus \dim V is the cardinality of the set and we are done. ♦

Note

Observe that the set \{(i,j,k) \in [n]^d : i\le j, i<k\} corresponds to the set of all SSYT with shape (2, 1) and entries in [n] (by writing i, j in the first row and k below i). This is an example of our earlier claim that a basis of V(\lambda) can be indexed by SSYT’s with shape \lambda and entries in [n]. For that, we will explore V(\lambda) as a quotient module of \otimes_j \text{Alt}^{\mu_j} V in the next article. This corresponds to an earlier article, which expressed S_d-irrep V_\lambda as a quotient of \mathbb{C}[S_d]b_T.

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Polynomials and Representations XXXV

Posted on June 27, 2016 by limsup

Schur-Weyl Duality

Throughout the article, we denote V = \mathbb{C}^n for convenience.

So far we have seen:

  • the Frobenius map gives a correspondence between symmetric polynomials in x_1, x_2, \ldots of degree d and representations of S_d;
  • there is a correspondence between symmetric polynomials in x_1, \ldots, x_n and polynomial representations of GL_n\mathbb C.

Here we will describe a more direct relationship between representations of S_d and polynomial representations of GL_n\mathbb{C}. Recall from earlier, that S_d and GL_n\mathbb C act on V^{\otimes d} as follows:

\begin{aligned} w\in S_d &\implies v_1 \otimes \ldots \otimes v_d \mapsto v_{w^{-1}(1)} \otimes \ldots \otimes v_{w^{-1}(d)},\\ g\in GL_n(\mathbb C) &\implies v_1 \otimes \ldots \otimes v_n \mapsto g(v_1) \otimes \ldots \otimes g(v_n),\end{aligned}

and the two actions commute, so w\circ g = g\circ w as endomorphisms of V^{\otimes d}.

Lemma. The subspace \text{Sym}^d V \subset V^{\otimes d} of all elements fixed by every w\in S_d is spanned by \{v^{\otimes d}: v\in V\}.

Proof

Use induction on d; the case d=1 is trivial so suppose d>1. For integers k\ge 0, consider the binomial expansion in \text{Sym}^d V:

\displaystyle(v + kw)^d = v^d + \left(\sum_{i=1}^{d-1} k^i {d\choose i} v^{d-i} w^{i}\right) + k^d w^d.

We claim: for large k, the (d+1)\times k matrix with (i, j)-entry j^i {d\choose i} (where 0\le i \le d) has rank d+1.

  • Indeed, otherwise there are \alpha_0, \ldots, \alpha_d \in \mathbb{C}, not all zero, such that \alpha_0 {d\choose 0} + \alpha_1 {d\choose 1} k + \ldots + \alpha_d {d\choose d} k^d = 0 for all large k, which is absurd since this is a polynomial in k.

Hence, we can find a linear combination summing up to:

\alpha_0 v^d + \alpha_1 (v+w)^d + \ldots + \alpha_k (v+kw)^d = vw^{d-1}, \qquad \text{ for all }v, w \in V.

Thus vw^{d-1} lies in the subspace spanned by all v^d. By induction hypothesis, the set of all w^{d-1} \in \text{Sym}^{d-1} V spans the whole space. Hence, the set of all v^d spans \text{Sym}^d V. ♦

This gives:

Proposition. If f: V^{\otimes d} \to V^{\otimes d} is an S_d-equivariant map, then it is a linear combination of the image of GL_n\mathbb{C} \hookrightarrow \text{End}(V^{\otimes d}).

Proof

Note that since \text{End}(V) \cong V\otimes V^\vee we have \text{End}(V^{\otimes d}) \cong \text{End}(V)^{\otimes d}. Hence from the given condition

f \in \text{End}(V^{\otimes d})^{S_d} = (\text{End}(V)^{\otimes d})^{S_d}.

By the above lemma, f is a linear combination of u^{\otimes d} for all u\in\text{End}(V). Since \text{GL}_n\mathbb{C} \subset \text{End}(V) is dense, f is also a linear combination of u^{\otimes d} for u\in \text{GL}_n\mathbb{C}. ♦

blue-lin

Main Statement

Now let U be any complex vector space and consider the complex algebra \text{End}(U). Recall: if A\subseteq \text{End}(U) is any subset,

C(A) = \{a \in \text{End}_{\mathbb C}(U) : ab = ba \text{ for all }b \in A\}

is called the centralizer of A. Clearly C(A) \subseteq \text{End}(U) is a subalgebra and we have A\subseteq C(C(A)).

Theorem (Schur-Weyl Duality). Let A\subseteq \text{End}(U) be a subalgebra which is semisimple. Then:

  • B:=C(A) is semisimple;
  • C(B) = A; (double centralizer theorem)
  • U decomposes as \oplus_{\lambda} (U_\lambda \otimes W_\lambda), where U_\lambda, W_\lambda are respectively complete lists of irreducible A-modules and B-modules.

Proof

Since A is semisimple, we can write it as a finite product \prod_\lambda \text{End}(\mathbb{C}^{m_\lambda}). Each simple A-module is of the form U_\lambda := \mathbb{C}^{m_\lambda} for some m_\lambda >0. As an A-module, we can decompose: \displaystyle U \cong \oplus_{\lambda} U_\lambda^{n_\lambda}. Here n_\lambda > 0 since as A-modules we have:

U_\lambda \subseteq A \subseteq \text{End}(U) \cong U^{\dim U}.

By Schur’s lemma \text{End}_A(U_\lambda, U_\mu) \cong \mathbb{C} if \lambda = \mu and 0 otherwise. This gives:

\displaystyle B = C(A) = \text{End}_A(U) = \text{End}_A\left(\prod_\lambda U_\lambda^{n_\lambda} \right) \cong \prod_\lambda \text{End}(\mathbb{C}^{n_\lambda})

which is also semisimple. Now each simple B-module W_\lambda has dimension n_\lambda. From the action of B on U, we can write U \cong \oplus_\lambda U_\lambda ^{n_\lambda} \cong \oplus_\lambda (U_\lambda \otimes W_\lambda) where A acts on the U_\lambda and B acts on the W_\lambda. Expressed as a sum of simple B-modules, we have U \cong \oplus_\lambda W_\lambda^{m_\lambda}; thus repeating the above with A replaced by B gives:

C(B) \cong \prod_\lambda \text{End}(\mathbb C^{m_\lambda})\cong A.

From A\subseteq C(C(A)) we thus have A= C(B). This proves all three properties. ♦

Note

From the proof, we see that

  • U = \oplus_\lambda (U_\lambda \otimes W_\lambda) as complex vector spaces,
  • A \cong \prod_\lambda \text{End}_{\mathbb{C}}U_\lambda acts on the U_\lambda, and
  • B\cong \prod_\lambda \text{End}_{\mathbb{C}} W_\lambda acts on the W_\lambda.

Thus the correspondence between U_\lambda and W_\lambda works as follows:

\begin{aligned}\text{Hom}_A(U_\lambda, U) &= \text{Hom}_{\prod \text{End}(U_\mu)}(U_\lambda, \oplus_\mu (U_\mu \otimes W_\mu))\\ &\cong \text{Hom}_{\text{End}(U_\lambda)} (U_\lambda, U_\lambda^{n_\lambda})\\ &\cong W_\lambda.\end{aligned}

The nice thing about this point-of-view is that the construction is now functorial, i.e. for any A-module M, we can define the corresponding: F: M \mapsto\text{Hom}_A(M, U). This functor is additive, i.e. F(M_1 \oplus M_2) \cong F(M_1) \oplus F(M_2), since the Hom functor is bi-additive.

blue-lin

The Case of Sd and GLnC

Now for our main application.

Consider S_d and GL_n\mathbb C acting on V^{\otimes d}; their actions span subalgebras A, B\subseteq \text{End}_{\mathbb C}(V). Now A is semisimple since it is a quotient of \mathbb{C}[S_d]. From the lemma, we have B = C(A) so Schur-Weyl duality says A = C(B), B is semisimple and

V^{\otimes d} \cong \oplus_\lambda (U_\lambda \otimes W_\lambda)

where U_\lambda, W_\lambda are complete lists of simple A– and B-modules respectively. Since A is a quotient of \mathbb{C}[S_d], the U_\lambda are also irreps of S_d so they can be parametrized by \lambda \vdash d.

Proposition. If U_\lambda is the irrep for S_d isomorphic to V_\lambda, then W_\lambda is the irrep for GL_n\mathbb{C} corresponding to V(\lambda).

Proof

It suffices to show: if \mathbb{C}[X_\lambda] corresponds to W' via the functor in the above note, then

W'\cong \text{Sym}^\lambda V = \text{Sym}^{\lambda_1} V \otimes \ldots \otimes \text{Sym}^{\lambda_l} V.

By definition W' = \text{Hom}_{S_d}(\mathbb{C}[X_\lambda], V^{\otimes d}). Recall that X_\lambda is a transitive S_d-set; picking a point A=(A_i) \in X_\lambda, any map f:\mathbb{C}[X_\lambda] \to V^{\otimes d} which is S_d-equivariant is uniquely defined by the element f(A)\in V^{\otimes d}, as long as this element is invariant under the stabilizer group:

H := \{w\in S_d : w(A) = A\} \cong S_{\lambda_1} \times S_{\lambda_2} \times \ldots \times S_{\lambda_l}.

Thus, the coefficients c_{i_1\ldots i_d} of e_{i_1}\otimes\ldots\otimes e_{i_d} in f(A) remain invariant when acted upon by \prod_i S_{\lambda_i}. So we have an element of \text{Sym}^\lambda V. ♦

Theorem. The set of irreps V_\lambda of S_d occurring in V^{\otimes d} is:

\{ V_\lambda : \lambda \vdash d, l(\lambda) \le n\}.

Proof

The following is the complete set of GL_n\mathbb{C}-irreps of degree d:

\{V(\lambda) : \lambda\vdash d, l(\lambda) \le n\}

We claim that this is also the set of all irreps in V^{\otimes d}. Clearly, each irrep in V^{\otimes d} is of degree d; conversely, V^{\otimes d} has

\psi = (x_1 + \ldots + x_n)^d = h_\mu(x_1, \ldots, x_n), \ \mu = (1,1,\ldots, 1).

Clearly K_{\lambda\mu} > 0 so V^{\otimes d} contains all V(\lambda) of degree d. Now apply the above proposition. ♦

Example

The simplest non-trivial example follows from the decomposition

V^{\otimes 2} = (\text{Sym}^2 V) \oplus (\text{Alt}^2 V).

The action of S_2 is trivial on the first component and alternating on the second.

Posted in Uncategorized | Tagged , , , , , , , | Leave a comment

Polynomials and Representations XXXIV

Posted on June 25, 2016 by limsup

Twisting

From the previous article, any irreducible polynomial representation of G= GL_n\mathbb{C} is of the form V(\lambda) for some \lambda \vdash d, l(\lambda) \le n such that \psi_{V(\lambda)} is the Schur polynomial s_\lambda(x_1, \ldots, x_n).

Now given any analytic representation V of G, we can twist it by taking V\otimes \det^k for an integer k. Then:

\displaystyle\psi_{V \otimes \det^k}= \psi_V \cdot \psi_{\det}^k = (x_1 \ldots x_n)^k \psi_V.

Twisting the irrep V(\lambda) with k\ge 0 gives us another irrep, necessarily of the form V(\mu). What is this \mu? Note that from \psi_{V(\lambda)} we can recover the partition \lambda by taking the minimal partition (with respect to \trianglelefteq). Hence from \psi_{V(\mu)} = (x_1\ldots x_n)^k\psi_{V(\lambda)} we must have \mu = \lambda + (k, \ldots, k). Thus:

Proposition. Any irreducible analytic representation of G can be uniquely written as:

\{\psi_{V(\lambda)} \otimes \det^k : l(\lambda) \le n-1, k\in\mathbb{Z}\}

where V(\lambda) is the polynomial representation satisfying:

\psi_{V(\lambda)} = s_\lambda(x_1, \ldots, x_n).

Since l(\lambda) \le n-1, s_\lambda(x_1, \ldots, x_n) is not divisible by x_n so the representation V(\lambda) \otimes \det^k is polynomial if and only if k\ge 0. Its degree is |\lambda| + kn.

blue-lin

Dual of Irrep

The dual of the irrep V(\lambda) is also a rational irrep, so it is of the form V(\mu) \otimes \det^k for some partition \mu with l(\mu) \le n-1 and integer k. From:

\psi_{V(\lambda)^\vee}(x_1, \ldots, x_n) = \psi_{V(\lambda)}(x_1^{-1}, \ldots, x_n^{-1})

we take the term with the smallest exponent for x^\mu in lexicographical order. For large N, denoting \text{rev}(\alpha) for the reverse of a sequence \alpha, we have:

\lambda, \mu \vdash d, \lambda \trianglerighteq \mu \implies \text{rev}((N,\ldots, N) - \lambda) \trianglerighteq \text{rev}((N,\ldots, N) - \mu).

Hence \mu = (\lambda_1, \lambda_1 - \lambda_{n-1},  \lambda_1 - \lambda_{n-2}, \ldots, \lambda_1 - \lambda_2) and k = -\lambda_1. Pictorially we have:

partition_of_dual_representation

Weight Space Decomposition

By definition \psi_{V(\lambda)} is the character of V(\lambda) when acted upon by the torus group S. Since this polynomial is s_\lambda = \sum_{\mu} K_{\lambda\mu} m_\mu, as vector spaces we have:

\displaystyle V(\lambda) = \bigoplus_{\mu} \bigoplus_{\sigma} V(\lambda)_{\sigma(\mu)}

where:

  • \mu runs through all partitions with |\mu| = |\lambda| and l(\mu) \le n;
  • \sigma(\mu) runs through all permutations of \mu without repetition, e.g. if \mu = (5, 3, 3) we get 3 terms: (5, 3, 3), (3, 5, 3) and (3, 3, 5);
  • V(\lambda)_{\nu} is the space of all v\in V(\lambda) for which S acts with character x^\nu, i.e.

V(\lambda)_{\nu} = \{v \in V(\lambda) : D(x_1, \ldots, x_n) \in S \text{ takes } v\mapsto x^\nu v\}

and the dimension of V(\lambda)_{\nu} is K_{\lambda\nu}. This is called the weight space decomposition of V(\lambda). We will go through some explicit examples later.

Foreshadowing: SSYTs as a Basis

As noted above, the dimension of V(\lambda)_{\sigma(\mu)} is exactly the number of SSYT with shape \lambda and type \sigma(\mu). Thus in a somewhat ambiguous way, we can take, as a basis of V(\lambda), elements of the form \{v_T\} over all SSYT T of shape \lambda and entries from [n]={1,2,…,n}; each v_T lies in the space V(\lambda)_{\text{shape}(T)}.

However, such a description does not distinguish between distinct SSYT of the same type. For that, one needs a construction like the determinant modules (to be described later).

blue-lin

Example: n=2

Consider G = GL_2\mathbb C. By the above proposition, each irreducible representation is given by V(m) \otimes \det^k where m, k are integers and m\ge 0. To compute V(m), we need to find a polynomial representation of G such that

\psi_{V(m)} = s_m(x, y)= x^m + x^{m-1}y + \ldots + y^m

corresponding to the SSYT with shape (m) and entries comprising of only 1’s and 2’s. E.g. s_4(x,y) = x^4 + x^3 y + x^2 y^2 + xy^3 + y^4 from:

gl2_example_ssyt

Such a V(m) is easy to construct: take \text{Sym}^m V; if {e, f} is a basis of V, then a corresponding basis of \text{Sym}^m V is given by \{e^i f^{4-i}\}_{i=0,\ldots,4}. If v_i := e^{2+i} f^{2-i}, then the diagonal matrix D(a, b) takes v_i \mapsto a^{2+i} b^{2-i} v_i so its character is a^4 + a^3 b + a^2 b^2 + ab^3 + b^4 as desired.

The weight space decomposition thus gives:

V(m) = V(m)_{4,0} \oplus V(m)_{3,1} \oplus V(m)_{2,2} \oplus V(m)_{1,3} \oplus V(m)_{0,4}

where each V(m)_{i,j} is 1-dimensional and spanned by e^i f^{4-i}.

Example: d=2

Consider G = GL_n\mathbb{C}. We have:

\mathbb{C}^n \otimes_{\mathbb C} \mathbb{C}^n \cong \text{Sym}^2 \mathbb{C}^n \oplus \text{Alt}^2 \mathbb{C}^n,

where each component is G-invariant. As shown earlier, we have:

\begin{aligned}\psi_{\text{Sym}^2} &= \sum_{1\le i\le j \le n} x_i x_j = h_2(x_1, \ldots, x_n),\\ \psi_{\text{Alt}^2} &= \sum_{1 \le i < j \le n} x_i x_j = e_2(x_1, \ldots, x_n).\end{aligned}

Since the Schur polynomials are s_2 = h_2 and s_{11} = e_2, both \text{Alt}^2 and \text{Sym}^2 are irreps of G. The weight space decomposition of the two spaces are:

\displaystyle \begin{aligned}\text{Sym}^2\mathbb{C}^n &= \bigoplus_{1\le i\le j\le n}\mathbb{C}\cdot e_i e_j, \\ \text{Alt}^2\mathbb{C}^n &= \bigoplus_{1\le i<j \le n}\mathbb{C} \cdot (e_i \wedge e_j).\end{aligned}

Hence in their weight space decompositions, all components have dimension 1.

blue-lin

Example: n=3

Now let us take G = GL_3\mathbb{C} and compute V(\lambda) where \lambda = (\lambda_1, \lambda_2) and \lambda_1 + \lambda_2 = d. To find s_\lambda(x,y,z) we need to compute K_{\lambda\mu} for all \mu\vdash d and l(\mu) \le 3. We will work in the plane X_1+ X_2+ X_3 = d; since partitions lie in the region X_1 \ge X_2 \ge X_3, we only consider the coloured region:

triangular_simplex

The point \lambda has \lambda_3 = 0. Assuming |\mu| = d, the condition \mu \trianglelefteq\lambda then reduces to a single inequality \mu_1 \le \lambda_1. Hence, \mu lies in the brown region below:

simplex_lambda_and_mu

To fix ideas, consider the case \lambda = (5,3). Calculating the Kostka coefficients gives us:

geometric_kostka_v2

Taking into account all coefficients then gives us a rather nice diagram for the weight space decomposition.

geometric_kostka_v1

E.g. we have \dim V(\lambda)_{2,3,3} =3 and \dim V(\lambda)_{4,3,1} = 2. These correspond to the following SSYT of shape (5,3):

weight_spaces_and_ssyt

blue-lin

Posted in Uncategorized | Tagged , , , , , , | Leave a comment