Minkowski Theory: Introduction
Suppose is a finite extension and
is the integral closure of
in K.
In algebraic number theory, there is a classical method by Minkowski to compute the Picard group of (note: in texts on algebraic number theory, this is often called the divisor class group; there is a slight difference between the two but for Dedekind domains they are identical).
We will only consider the simplest cases here to give readers a sample of the theory.
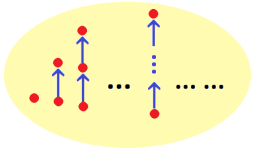
Minkowski’s Lemma.
If a measurable region
has area > 1, then there exist distinct
such that
.
Proof
Use the following picture:
Since the area > 1, there exist two points which overlap in the unit square on the right. The corresponding then give
. ♦
Minkowski’s Theorem.
Let
be a measurable region which is convex, symmetric about the origin and has area > 4. Then X has a lattice point other than the origin.
Proof
Take , which has area > 1. By Minkowski’s lemma, there exist distinct
such that
. Since X is symmetric about the origin replace y by –y (so
) to give
. And since X is convex,
. Finally since
,
is not the origin. ♦
By applying a linear transform to we obtain the more useful version of Minkowski’s theorem.
Minkowski’s Theorem B.
Take a full lattice
(i.e. discrete subgroup which spans
). Taking a basis
of L, we obtain a fundamental domain
of area D. If
is convex, symmetric about the origin, and has area > 4D, then X has a non-zero point of L.

Picard Group of Number Rings
Now we use this to compute for
.
First note that any non-zero ideal has finite index since if
, then
is a non-zero integer in
so
, where N is the norm function. We let
.
Recall that if , by proposition 4 here, the composition factors of
comprise of exactly
copies of
for each i, so
In particular, for any non-zero ideals
, and we can extend the norm function to the set of all fractional ideals of A.
Exercise
Prove that if then
so we can consider as an extension of the norm function to the set of ideals.
To apply Minkowski’s theorem B, we identify with
. Let
be any non-zero ideal with norm N, considered as a full lattice in
. We take
where t will be decided later. Note that S is convex, symmetric about the origin and has area . If
where
then Minkowski’s theorem B assures us there exists
with
. Since this holds for all
we have:
Now has norm
, i.e.
. Hence every element of Pic A can be represented by an ideal
of norm 1 or 2. Since A has norm 1 and
has norm 2, we have proven:
.
More generally, one can show the following.
Theorem.
Let
be a finite extension. Then the Picard group of
is finite; its cardinality is called the class number of K.
Exercise
Prove that has class number 3. Note that
.
Prove that has class number 1.
Prove that has class number 2.
[ Hint: identify with
. Pick the square
for a suitable t. You could also pick
but it is not as efficient. ]

Geometric Example: Elliptic Curve Group
Take the elliptic curve E over given by
and let
be its coordinate ring. In Exercise B.1 here, we showed A is a normal domain. Clearly it is noetherian. By Noether normalization theorem,
. Hence, A is a Dedekind domain.
We will show how computation of Pic A leads to point addition on the elliptic curve. For each maximal ideal , write
for its image in Pic A. Recall that points
correspond bijectively to maximal ideals
.
Lemma 1.
Suppose
is not a unit. Then taking
as a complex vector space,
if and only if
can be represented by a linear function in X, in which case
for some
.
Note
The intuition is that the curve and the elliptic curve cannot have less than 3 intersection points (with multiplicity) unless we take a vertical line.
Proof
Since in the ring A, without loss of generality we can write
for . The condition
implies
and
have at most two intersection points. Solving gives us
.
If , the LHS has odd degree while the RHS has even degree; hence the equation has at least 3 roots and each corresponds to at least one point on the elliptic curve. If
and
, then
so
is linear in X, and we are done. ♦
Exercise
If we replace by a general algebraically closed field k, would the proof still work? What additional conditions (if any) need to be imposed?
Corollary 1.
No maximal ideal of A is principal.
Proof
If is generated by f then
, which is impossible by lemma 1. ♦
Corollary 2.
For any points
and
on E,
is principal if and only if
When that happens, we write
.
Proof
(⇐) If then setting
gives
If , this ring has exactly two maximal ideals, corresponding to maximal ideals
and
of A. If
, it has exactly one maximal ideal so we still have
.
(⇒) If is principal, then
so by lemma 1, f can be represented by a linear function in X so we must have P and Q as described. ♦
Corollary 3.
If
satisfy
, then
.
Proof
Let as in corollary 2. Then
. By the given condition
so by corollary 2 again we have
and hence
. ♦
Lemma 2.
For any
with
, there is a unique
such that
Proof
First suppose so P and Q have different x-coordinates. Let
be the equation of PQ. We get:
which has complex dimension 3. Since is divisible by
we have
for some
. Geometrically R is the third point of intersection of PQ with E, which can be equal to P or Q.
If with
, we can similarly pick a line through P of gradient
. Then as above
where
has a double root for
(this requires some algebraic computation). Hence
for some
. ♦
Summary.
The Picard group of A is given by
.
In particular it is infinite.




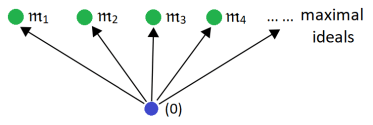

 However, even in a catenary ring A, not all maximal prime chains may be of the same length. The reason is rather simple: A can have multiple minimal prime ideals and multiple maximal ideals. The catenary condition does not specify that every saturated prime chain from every minimal prime to every maximal prime must be of the same length.
However, even in a catenary ring A, not all maximal prime chains may be of the same length. The reason is rather simple: A can have multiple minimal prime ideals and multiple maximal ideals. The catenary condition does not specify that every saturated prime chain from every minimal prime to every maximal prime must be of the same length.