Catenary Rings
Let us look at prime chains in greater detail.
Definition.
Let
be a chain of prime ideals of a ring A. We say the chain is
- saturated if for any prime ideal
of A,
;
- maximal if it is saturated,
is a minimal prime and
is a maximal ideal.
In words, saturated means we cannot insert a prime ideal between any two consecutive terms of a chain; maximal means in addition, we cannot extend the chain further in either direction.
Definition.
A ring is said to be catenary if, for all primes
, all saturated prime chains with fixed ends
have the same length d.

Note
If A is a catenary ring, so is any of its quotient or localization
since the resulting spectrum is a subspace of Spec A.

Clarifications
Since dimension theory can be rather tricky, we will spend some time to clarify some of the above concepts.
1. On Catenary Rings
Catenary rings A are extremely common. In fact, it takes quite a bit of effort to construct a noetherian ring which is not catenary and such examples are usually pathological. See this article from Stacks project for an explicit construction by Nagata.
2. Maximal Prime Chains in Catenary Rings
 However, even in a catenary ring A, not all maximal prime chains may be of the same length. The reason is rather simple: A can have multiple minimal prime ideals and multiple maximal ideals. The catenary condition does not specify that every saturated prime chain from every minimal prime to every maximal prime must be of the same length.
However, even in a catenary ring A, not all maximal prime chains may be of the same length. The reason is rather simple: A can have multiple minimal prime ideals and multiple maximal ideals. The catenary condition does not specify that every saturated prime chain from every minimal prime to every maximal prime must be of the same length.
E.g. in the following Spec A, the blue prime chains may be longer than the green ones.

With multiple minimal primes, it is easy to construct catenary rings with maximal prime chains of different lengths. For example if , the set of prime chains of B is the union of that of
and of
. So if we pick
of different dimensions like
we get maximal prime chains of different lengths:
.
3. Catenary Rings Which Are Integral Domains
What if we specify that A is an integral domain? This ensures that there is a unique minimal prime: 0 itself. There remains the possibility of multiple maximal ideals. When A is a finitely generated algebra over a field, indeed all maximal prime chains have the same length (to be proven later).
In the general case, we have the following counter-example where
. This has maximal prime chains
of different lengths.
4. Dimension of Noetherian Rings
If A is a noetherian ring, every chain of ideals of A must eventually terminate so we cannot have infinite prime chains. But this does not mean must be finite, for A may have maximal prime chains of arbitrary length. For example, Nagata constructed a noetherian ring A whose spectrum looks like the following,

where the i-th column is a maximal prime chain of length i-1. In particular, .
Exercise A
1. Decide if each of the following is true or false.
- If A is a catenary ring which is a local integral domain, then all maximal prime chains have the same length.
- If A is a catenary ring which is a local ring, then all maximal prime chains have the same length.
2. Let A be a noetherian domain.
- Prove that if the prime ideal
of A is principal, then it is a minimal non-zero prime.
- Prove that if A is a UFD, any minimal non-zero prime ideal is principal.
3. Prove that the two prime chains in example 3 are maximal.
4. Prove that any maximal prime chain of has length 2. In particular,
is catenary and hence the ring in example 3 is catenary since it is a localization of
.

More Consequences of NNT
Now we consider finitely generated k-algebras where k is a field.
Proposition 1.
Let
. All maximal prime chains of A have the same length n.
Note
Although we already have dim A = n, this is a significantly stronger result.
Proof
The proof is by induction on n. We may assume .
Note that 0 is a prime ideal of A. Let be a minimal non-zero prime and
. By exercise A.2 above
since A is a UFD. By exercise B here, B has transcendence degree n – 1 so by induction hypothesis any maximal prime chain of B has length n – 1. Since
is an arbitrary minimal non-zero prime this shows that any maximal prime chain of A has length n. ♦
With this as a base, we may now prove the more general result.
Proposition 2.
Let A be a finitely generated k-algebra which is also an integral domain. All maximal prime chains of A have the same length n.
Note
We must have .
Proof
Since A is finitely generated we can write it as for a prime ideal
. Fix a saturated prime chain of
which starts at 0 and ends at
; let j be its length.
Now suppose we pick any maximal prime chain of A; let l be its length. The chain must start at 0 and end at a maximal ideal, which corresponds to a prime chain of starting at
and ending at a maximal ideal (containing
). Appending the prior chain, we thus obtain a maximal prime chain of
. By proposition 1, we must have
so
is independent of the maximal prime chain of A we chose. ♦

Height of an Ideal
Definition.
Let
be a prime ideal. The height of
, denoted by
, is the supremum of the lengths of prime chains ending at
.
In other words . Since
is the supremum of the lengths of prime chains starting from
, it follows that we always have
We can also define the height of any ideal.
Definition.
Let
be an ideal. The height of
, denoted by
, is the infimum of
over all primes
.
Note
Here is the intuition behind the definition. Note that is the supremum of
over all
. Thus to “compensate” for taking the supremum here, we let
take the infimum of
over all
.
From the previous section, we obtain:
Corollary 1.
If A is a finitely generated k-algebra and also an integral domain, then for any prime ideal
we have
In particular, A is a catenary ring.
More generally we have:
Corollary 2.
Any finitely generated algebra A over a field is catenary.
Hence so is any localization of such an algebra.
Proof
A must be a quotient of some so it is catenary. ♦


Is it not required to add the following at the end of the first paragraph of the proof of Proposition 2? : The local ring![k[X_1, \ldots, X_m]_{\mathfrak{p}}](https://s0.wp.com/latex.php?latex=k%5BX_1%2C+%5Cldots%2C+X_m%5D_%7B%5Cmathfrak%7Bp%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a local domain so all maximal chains have the same length. Therefore the corresponding saturated prime chains which starts at
is a local domain so all maximal chains have the same length. Therefore the corresponding saturated prime chains which starts at 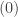 and ends at
and ends at 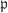 have the same length.
have the same length.
Actually I don’t need to add that statement, although it’s true. By the end of the proof, it also follows that all saturated prime chains starting at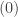 and ending at
and ending at  are of the same length.
are of the same length.