Skew Diagrams
If we multiply two elementary symmetric polynomials and
, the result is just
, where
is the concatenation of
and
sorted. Same holds for
However, we cannot express
in terms of
easily, which is unfortunate since the Schur functions are the “preferred” basis, being orthonormal. Hence, we define the following.
Definition. A skew Young diagram is a diagram of the form
, where
and
are partitions and
for each
E.g. if and
then

Note that the same skew Young diagram can also be represented by where
and
These two Young diagrams are considered identical.
Definition. A skew semistandard Young tableau (skew SSYT) is a labelling of the skew Young diagram with positive integers such that each row is weakly increasing and each column in strictly increasing. Now
is called the shape of the tableau and its type is given by
where
is the number of times
appears.
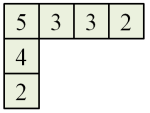
E.g. the following is a skew SSYT of the above shape. Its type is (4, 1, 1, 1).


Skew Schur Polynomials
Definition. The skew Schur polynomial corresponding to
is given by:
where
is
. E.g. the above diagram gives
The proof for the following is identical to the case of Schur polynomials.
Lemma. The skew Schur polynomial
is symmetric.
Indeed, one checks easily that the Knuth-Bendix involution works just as well for skew Young tableaux.

So the number of skew SSYT of shape and type
is unchanged when we swap
and
Example
For and
, we have:

The following result explains our interest in studying skew Schur polynomials.
Lemma. The product of two skew Schur polynomials is a skew Schur polynoial.
For example, we have:

It remains to express as a linear combination of
, where

Littlewood-Richardson Coefficients
Recall that we have Pieri’s formula , where
is summed across all diagrams obtained by adding
boxes to
such that no two are on the same column. Repeatedly applying this gives us:
where and
is obtained from
by adding
boxes such that no two lie in the same column. Hence, the number of occurrences for a given skew Young diagram
is the number of skew SSYT’s with shape
and type
Example
If and
, here is one way of appending 4, 2, 1 boxes in succession:

which corresponds to the following skew SSYT:

This gives us the tool to prove the following.
Theorem. For any
with
, we have:
so the linear map
is left adjoint to multiplication by
Proof
It suffices to prove this for all where
Since
is the basis dual to
, the LHS is the coefficient of
in expressing
in terms of monomial symmetric polynomials. By definition of
, this is equal to the number of skew SSYTs with shape
and type
; we will denote this by
the skew Kostka coefficient.
By the reasoning above, when is expressed as a linear combination of Schur functions, the coefficient of
is also
. Since the Schur functions are orthonormal, we are done. ♦
Note
The theorem is still true even when does not all hold, if we take
. Indeed, by reasoning with Pieri’s rule again, every Schur polynomial
occuring in
must have
for all
Definition. When we express:
the values
are called the Littlewood-Richardson coefficients.
By the above theorem, this equals One can calculate this using the Littlewood-Richardson rule, which we will cover later.



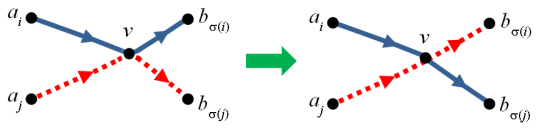





 However, the involution
However, the involution 












 In the above diagram a → b means that b can be expressed as a polynomial in a with integer coefficients; the same holds for dotted arrows but now the polynomial may have rational coefficients.
In the above diagram a → b means that b can be expressed as a polynomial in a with integer coefficients; the same holds for dotted arrows but now the polynomial may have rational coefficients.