Filtered Rings
Definition.
Let A be a ring. A filtration on A is a sequence of additive subgroups
such that
for any
. A filtered ring is a ring with a designated filtration.
Note
Since , in fact each
is an ideal of A.
Examples
1. If is a grading, we can form a filtration by taking
(where
refers to the grading).
2. Let be an ideal. The
–adic filtration is given by
. E.g. we can take
and
, then
is the set of integers divisible by
. More generally, in a dvr with uniformizer
, we can take
.
Definition.
Suppose A is a filtered ring. A filtration on an A-module M is a sequence of additive subgroups
such that
for any
. A filtered module is a module with a designated filtration.
Note
Since , each
is an A-submodule of M.
Also, we need a fixed filtration on the base ring A before we can talk about filtrations on A-modules.
Example
Again, for an ideal , we obtain the
–adic filtration of M, where
.

Induced Filtrations
For the rest of this article, A denotes a filtered ring.
Definition.
Let M, N be filtered A-modules. A linear map
is said to be filtered if
for each i.
We also have:
Definition.
Let
be a linear map of A-modules.
- If
is a filtration of M, the induced filtration on N via f is given by
.
- If
is a filtration of N, the induced filtration on M via f is given by
.
Note
Let us show that the induced filtrations are legitimate. In the first case,
.
And in the second,
In particular, if M is a filtered A-module and is a submodule, the induced filtrations on N and M/N are given by:
So far everything is natural, but beneath all this a danger lurks.
 If
If is a filtered A-linear map, then
and
have induced filtrations via quotient module of M and submodule of N. Although
as A-modules, it is not an isomorphism in the category of filtered A-modules!
Let us write everything out explicitly. The filtration on the LHS and RHS are given respectively by
which gives
which is not isomorphic to in general.

Completion
Definition.
Let M be a filtered A-module, the completion of M is the following (inverse) limit of A-modules:
By the description of inverse limits in the category of A-modules, comprises of the set of all
such that for each i,
maps to
under the canonical map
.
The canonical maps induce an A-linear map
by the universal property of inverse limits. This can be described as follows: for each
, let
be its image in
; then the map takes
. From this we see that:
Lemma 1.
The map
is injective if and only if
, in which case we say the filtration is Hausdorff.
Next, by setting M = A, we also have . Although we defined
as an A-module, one sees by the explicit construction that
has a ring structure. To be specific,
Exercise A
1. Prove that has a canonical structure as an
-module.
2. Prove that is the inverse limit of
in the category of rings. In particular, the canonical map
is a ring homomorphism.
3. Prove that if the filtration on M is Hausdorff, we can define a metric on M via:
, where
such that the collection of all cosets forms a basis for the resulting topology. In fact, d is an ultrametric.

Limits in Completion
The completion enables us to take limits of infinite sequences and sums of infinite series in modules.
Definition.
Let
be a sequence in a filtered module M. We say the sequence is Cauchy if: for any i, there exists n such that
.
The astute reader would note that if the filtration is Hausdorff, then is Cauchy here if and only if it is Cauchy with respect to the metric of exercise A.3.
Definition.
The limit of a Cauchy sequence
is defined as follows. For each i, pick n such that
modulo
, with image
. Now define:
.
From the definition, it is clear that if (resp.
) are Cauchy sequences in M (resp. in A), then
and
are also Cauchy and we have
Example: 𝔪-adic Completion
Pick a ring A with maximal ideal ; we will take the
-adic filtration
. Given a sequence
for
, let
, an element of
.
Then is a Cauchy sequence in A and we write:
.
Arithmetic Example.
Let and
for a prime p. The completion
is called the ring of p-adic integers and denoted by
. Let us take p = 2 and the element:
Then is congruent to -1 modulo any
. Thus
. In general, an element of
can be regarded as having an infinite base-p expansion. Thus the above
would have base-2 expansion
. One easily checks that three times this value is
, which is -1.
Geometric Example
Let A be a ring, and
where
. Again, we can take the infinite sum
and check that
. Note that
, the ring of formal power series with coefficients in A.
Definition.
Let A be any ring. A formal power series in X with coefficients in A is an expression
, where
.
Unlike polynomials, we allow infinitely many
to be non-zero. Addition and multiplication of formal power series are defined as follows. For
and
,
This gives a ring structure on the set
of formal power series. To define rings of formal power series in multiple variables, we set recursively
As another example, let us take the -adic completion for
and
. We will prove later that
and that the map is an isomorphism. Geometrically, this means when we project
to the Y-axis, the map is locally invertible at the origin.

[ Image edited from GeoGebra plot. ]
 Functorially, the ring
Functorially, the ring behaves quite differently from
, because as an A-module, it is a countably infinite direct product of copies of A, unlike
which is a direct sum. If we follow the earlier guideline, it is (for example) generally false that
for any A-algebra B.
Exercise B
1. Prove that the canonical map is not an isomorphism.
2. Let A be a filtered ring. Prove that if is
, then f defines a map
Prove that if we fix , we get a ring homomorphism
,
.



In the first definition in the section “Limits in completion” it is mentioned that “Let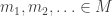 , but in the congruences immediately following that sentence
, but in the congruences immediately following that sentence 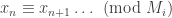 .
.
The scalar multiplication just before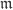 -adic completion has a typo.
-adic completion has a typo.
Thanks! Corrected this error and the earlier one.
What does “locally invertible at the origin” in the diagram mean?
This one should be regarded as just a form of geometric intuition. If we “zoom in” the graph at the origin, eventually it resembles a straight line. For a non-example, if we “zoom in” the graph of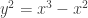 or
or 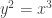 at the origin, you will see a singularity there.
at the origin, you will see a singularity there.
This sounds familiar: you might have seen this earlier for localization, but the completion takes the intuition one step further. For example, the completion of![A = \mathbb C[X, Y]/(Y^2 - X^3 + X)](https://s0.wp.com/latex.php?latex=A+%3D+%5Cmathbb+C%5BX%2C+Y%5D%2F%28Y%5E2+-+X%5E3+%2B+X%29&bg=ffffff&fg=333333&s=0&c=20201002) at the origin is in fact isomorphic to
at the origin is in fact isomorphic to ![\mathbb C[[Y]]](https://s0.wp.com/latex.php?latex=%5Cmathbb+C%5B%5BY%5D%5D&bg=ffffff&fg=333333&s=0&c=20201002) yet the localization of
yet the localization of  at the origin is not the localization of a polynomial ring.
at the origin is not the localization of a polynomial ring.