Direct Sums and Direct Products
Recall that for a ring A, a sequence of A-modules gives the A-module
where the operations are defined component-wise. In this article, we will generalize the construction to an infinite collection of modules. Throughout this article, let
denote a collection of A-modules, indexed by
.
Definition.
The direct product
is the set-theoretic product of the
, with the structure of an A-module given by:
.
The direct sum
is the submodule of
comprising of all
such that
only for a finite number of
.
Since there are only finitely many non-zero terms for an element , one often writes the element additively, i.e.
.
For a simple example, note that if for a fixed module M, then
is the set of all functions
. On the other hand,
is the set of all f such that
for only finitely many
. [We say f has finite support.]
Exercise A
For an infinite collection of A-modules and an ideal
, which of these claims is true?
[Note: if it seems too hard to find a counter-example, argue qualitatively why equality does not hold.]

Universal Property
At first glance, it seems like the direct product is the right definition since it generalizes directly from direct product of groups, rings, topological spaces etc. However, generally the direct sum is better behaved for our needs. The above exercise should provide some evidence of that.
For now, we will show that the direct sum and direct product are actually dual of each other, by showing the corresponding universal properties.
Theorem (Universal Property of Direct Product).
Let
. For each
, take the projection map
Now the collection of data
satisfies the following.
- For any A-module N and collection of data
where each
is A-linear, there is a unique A-linear
such that
for each
.
Note
The idea is that homomorphisms “classify” the collection of all I-indexed tuples
.

Proof.
For existence, define to be
. Now for any
we have
.
For uniqueness, if , the j-th component of
is
so the tuple
must be
. ♦
The following result shows why universal properties are important.
Proposition 1.
Let M’ be an A-module and
be a collection of data satisfying the above universal property. Then there is a unique isomorphism
such that
for all
.
Proof
1. We apply the universal property to and
for each i. There exists a unique
such that
. We know one such f, namely
. Hence this is the only possibility.
2. Next apply the universal property to N = M’ and . There exists a unique
such that
for each i.
3. But we know also satisfies this same universal property. Swapping M and M’ there exists a unique
such that
for each i.
4. Now for each i. By step 1, we have
. By symmetry we get
too. ♦
Note
In fact, we have proven something stronger: that there is a unique homomorphism such that
for all i and this f must be an isomorphism.

Direct Sum
Similarly, the direct sum satisfies the following.
Theorem (Universal Property of Direct Sum).
Let
. For each
, take the embedding
Thus
has component
at
and 0 if
. The collection of data
satisfies the following.
- For any A-module N and collection of data
where each
is A-linear, there is a unique A-linear
such that
for each
.
Proof.
Left as an exercise. ♦
We also have uniqueness for the above universal property.
Proposition 2.
Let M’ be an A-module and
be a collection of data satisfying the above universal property. Then there is a unique isomorphism
such that
for each
.
Proof.
Left as an exercise. ♦
The following exercise tests your conceptual understanding of universal properties.
Important Exercise
Suppose we messed up and take the following maps instead:
- embeddings
which take
to
;
- projections
which take
to
.
Explain why fails the universal property of direct sum, and
fails the universal property of direct product.
[Hint (highlight to read): one of them fails the uniqueness property, the other fails the existence property.]

Optional Example
Let I be the set of all primes. Consider the direct sum of -modules
. Consider the
-linear homomorphism (i.e. additive homomorphism)
Note that addition is well-defined because only finitely many are non-zero. Also,
is independent of our choice of integer
.
The map is injective: suppose where
are distinct primes and each
. Multiplying throughout by
gives
where each term in brackets is divisible by . Since
is coprime to
we have
which is a contradiction.
Claim: the image of the map is the set G of all rational where n is square free. Indeed, suppose n in
is square free; write
as a product of distinct primes.
- Now the subgroup
of G has order n.
- On the other hand, the submodule
maps into G injectively with image with
.
- Since
, we see that
lies in the image.
Thus .


Thank you for your beautiful notes. Can you give some references of your notes?
Hi. Some common references for Commutative Algebra include:
– R. Y. Sharp, “Steps in Commutative Algebra” (possibly the easiest book to read among this list).
– Atiyan & Macdonald, “Introduction to Commutative Algebra” (well-written but extremely terse).
– David Eisenbud, “Commutative Algebra: With a View Toward Algebraic Geometry” (more advanced than the previous two books but has loads of nice examples and exercises, a bit verbose though).
– Hideyuki Matsumura, “Commutative Ring Theory” (possibly the most advanced in this list, a good follow-up to A & M).
But it’s best to supplement your reading of commutative algebra with some algebraic geometry. “Algebraic Curves” by Fulton is a nice introduction to the topic.
There is. map missing in in the important exercise, though it is obvious what you mean.
in the important exercise, though it is obvious what you mean.
Also did you mean in “Since
in “Since  is coprime to
is coprime to 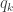 we have
we have  which is a contradiction.
which is a contradiction.
Thank you for all the bug fixes. 😀
I enjoy your exposition very much. Hope you don’t mind my comments.