Topology: Basic Definitions

Motivation and Definition

While studying analysis, one notices that many important concepts can be defined in terms of “open sets”. One gets the inkling that this concept is critical in forming our notions of continuity, limits etc. In this article, we shall abstractise this further by considering only open sets. At first glance, it does seem rather unlikely that such a general definition could be useful in any manner. However, it will soon become clear that abstractisation has the following advantages:

It brings out the essence of proofs of theorems, by highlighting specific properties of an object which are critical to the proofs.
The concepts can be applied to vastly different areas of mathematics, including for example, number theory, Galois theory, commuative algebra (in more ways than one!) etc, and have proven to be extraordinarily fruitful in furthering their study.

Enough talk, let’s begin. Let X be any set. As mentioned above, we wish to define a topology on it by stating what constitutes “open sets”.

Definition. Let $\mathbf{P}(X)$ be the power set of X (i.e. set of all subsets of X). A topology on X is a subset $T\subseteq \mathbf{P}(X)$ satisfying:

$\emptyset, X \in T$ ;

if $U_1, U_2 \in T$ , then $U_1 \cap U_2\in T$ ;

if $U_i\in T$ is a collection of elements of T, then $\cup_i U_i\in T$ .

If U is a subset of X belonging to T, we say U is an open subset of X. If C is a subset of X whose complement X-C belongs to T, we say C is a closed subset of X.

Some observations:

The definition does not preclude the possibility that a subset can be both open and closed, so the terminology is a little unfortunate. For a quick motivation of why closed subsets are of interest, read here.
By repeatedly applying intersection, one notes that if $U_1, U_2, \ldots, U_n$ are open, then so is $U_1\cap U_2\cap\ldots\cap U_n$ . In other words, a topology is closed under an intersection of finitely many terms, but not infinitely many terms in general (see the example of R later, where the intersection of all $U_n = (-\frac 1 n, +\frac 1 n)$ is {0}, which is not open).

Note that we could also define a topology by stating what constitutes “closed subsets” of X. Thus:

$\emptyset, X$ are closed subsets of X;
if $C_1, C_2$ are closed subsets of X, then so $C_1 \cup C_2$ is closed;
if $C_i$ is a collection of closed subsets of X, then $\cap_i C_i$ is closed.

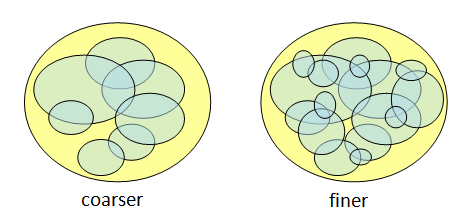
Definition. Suppose $T_1, T_2$ are both topologies on X. If $T_1\subseteq T_2$ , then we say $T_2$ is a finer topology than $T_1$ and conversely $T_1$ is a coarser topology than $T_2$ .

[ Note: this diagram is meant as an illustration of finer/coarser; it does not represent actual topologies. ]

Examples of Topologies

On any set X, we have the discrete topology T = P(X) where every subset is open; this is the finest topology possible for X. Also, there’s the trivial topology $T=\{\emptyset, X\}$ , which is the coarsest topology possible for X.
Let $X=\mathbf{R}^n$ . The standard topology on X was already defined earlier. Recall that $U\subseteq X$ is open if and only if for each x in U, there is an ε>0, such that any y in X satisfying |y – x|<ε must be in U also.
Let X be a set. The cofinite topology is defined via having $U\subseteq X$ open if and only if X–U is finite. In other words, the class of closed subsets is precisely the class of finite subsets, from which it’s clear that the cofinite topology satisfies the set of axioms of a topology.
Let N = {1, 2, … } be the set of positive integers. The right order topology on N is where the only non-empty open subsets are $U_m = \{m, m+1, m+2, \ldots\}$ for m=1, 2, 3, … . Note that $U_m \cap U_n = U_{\max(m,n)}$ and $\cup_i U_{m_i} = U_{\min(m_i)}$ ; the fact that the order topology is closed under arbitrary union follows from that every subset of N has a minimum.
If $\mathbf{N}^* = \mathbf{N}\cup\{\infty\}$ , where ∞ is just a dummy symbol here, then we can define a topology on N* by decreeing that the only non-empty open subsets are $U_m^* = U_m \cup\{\infty\}.$ Thus, any open subset containing ∞ contains all sufficiently large natural numbers.

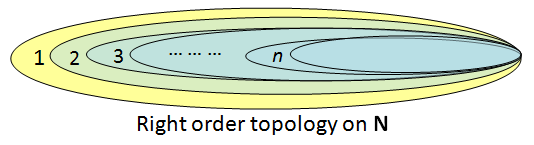[ Side note: more generally, one can define the order/right-order and left-order topology on any totally ordered set. Note that the right-order topology on N* differs from the one described in example 5, since {∞} is an open subset in the right-order topology. ]

Metric Spaces

One common source of topologies is via a metric function, which provides a geometry by indicating the “distance” between any two points in a set.

Definition. A metric on a set X is a function $d:X\times X\to\mathbf{R}$ such that:

d(x, y) ≥ 0 for any x, y in X, with equality if and only if x=y;

d(x, y) = d(y, x) for any x, y in X;

d(x, z) ≤ d(x, y) + d(y, z) for any x, y, z in X (triangular inequality).

The pair (X, d) is then called a metric space.

The triangular inequality ensures that the function d behaves like a “distance function”.

Examples

The discrete metric on any X is defined by d(x, y) = 0 if x=y and 1 otherwise.
Let $X=\mathbf{R}^n$ . The Euclidean metric is the standard distance function $d(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$ .
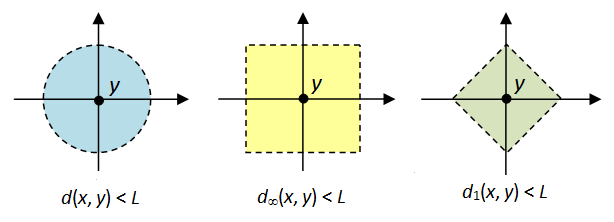
Let $X=\mathbf{R}^n$ again. This time we take the metrics $d_1(x,y)=\sum_{i=1}^n |x_i - y_i|$ and $d_\infty(x,y)=\max_{i=1}^n |x_i - y_i|$ . [ See diagram below. ]
Let p be a prime number and X=Z, the set of integers. Given any integer m let where is the highest power of p dividing m; in the case m=0, since all powers of p divide m we have . Then is a metric, called the p-adic metric on Z. This was briefly alluded to in a prior post. [ Note: the triangular inequality follows from the fact that if divides both x–y and y–z, then it divides x–z. One way of looking at this metric is that two integers are near if their difference is divisible by a high power of p. ]
- E.g. suppose p=5. Then d(5, 3)=|5-3|₅ = 0, d(57, -18)=|75|₅ = 1/25, and d(152, 27) = 1/125.

The following theorem shows that a metric space gives rise to a topology.

Theorem. Let (X, d) be a metric space. For x in X and ε>0, the open ball with radius ε>0 and centre x is defined by

$N(x, \epsilon) = \{y\in X: d(x, y)<\epsilon\}.$

We say that a subset $U\subseteq X$ is open if for any x in U, there is an open ball $N(x,\epsilon)\subseteq U$ for some ε>0. Then the collection of open sets form a topology.

[ Note: the above diagrams for d, d₁ and d_∞ illustrate the open balls for the respective metrics. ]

Proof.

Clearly, $\emptyset$ and X are both open. Now, suppose $U_1, U_2\subseteq X$ are open (in the sense of metric space). If $x\in U_1\cap U_2$ , then x lies in both U₁ and U₂. Thus, we can find $\epsilon_1, \epsilon_2>0$ such that:

$N(x, \epsilon_1) \subseteq U_1$ and $N(x,\epsilon_2)\subseteq U_2$ .

So $N(x, \min(\epsilon_1, \epsilon_2)) \subseteq N(x,\epsilon_1)\cap N(x,\epsilon_2) \subseteq U_1 \cap U_2$ .

Finally for arbitrary union of open subsets, let $U_i\subseteq X$ be open and $U = \cup_i U_i$ . If x lies in U, then it must lie in some U_i. Thus, for some ε>0, $N(x,\epsilon) \subseteq U_i \subseteq U$ . ♦

For example,

the above metric space $(\mathbf{R}^n, d)$ induces the topology on Rⁿ defined earlier;
the discrete metric on any set X induces the discrete topology;
the open ball N(x, ε) itself is an open subset of X (the proof is an exact replica of the one in an earlier post, by replacing |x–y| with d(x, y)).

We say that a topology (X, T) is metrisable if there’s a metric d on X which induces it. But even if such a d exists, it is usually far from unique. For example, the above metrics d, d₁ and d_∞ on Rⁿ all induce the same topology as we will show a short while later.

Definition. Two metrics d and d’ on X are said to be topologically equivalent if they induce the same topology.

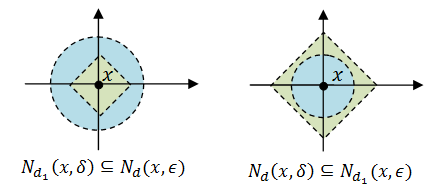
Theorem. This happens if and only if:

for any x in X and ε>0, there exists δ>0 such that $N_{d'}(x,\delta) \subseteq N_d(x, \epsilon)$ ;

for any x in X and ε>0, there exists δ>0 such that $N_{d}(x,\delta) \subseteq N_{d'}(x, \epsilon)$ ;

[ Since there’re two metrics here, we use the subscript N_d to denote the open ball induced by d. ]

Proof

Suppose d and d’ induce topologies T and T’ respectively. It suffices to show that the first condition is equivalent to that T’ is finer than T.

For the forward direction, suppose $U\in T$ , i.e. it is open in the metric space (X, d). Then for any x in U, $N_d(x, \epsilon)\subseteq U$ for some ε>0. By the first condition, $N_{d'}(x, \delta)\subseteq N_d(x,\epsilon)$ for some δ>0. Hence it follows that U is open in the metric space (X, d’) too.

For the converse, suppose let x be in U and ε>0. Then since $U:=N_d(x,\epsilon)$ is open in T, it is also open in T’. Hence $N_{d'}(x,\delta)\subseteq U$ for some δ>0. ♦

For example, the following diagram shows that d₁ and d are topologically equivalent on Rⁿ.

Conclusion: every metric space induces a topology and many different metrics on the same space can induce the same topology. We’ll see later that some topologies are inherently non-metrisable.