Burnside’s Lemma and Polya Enumeration Theorem (2)

[ Acknowledgement: all the tedious algebraic expansions in this article were performed by wolframalpha. ]

Counting Graphs

One of the most surprising applications of Burnside’s lemma and Polya enumeration theorem is in counting the number of graphs up to isomorphism.

Problem. Find the number of simple graphs with n vertices, up to isomorphism.

Let V be a set of n vertices, and E be the set of all 2-element subsets of V. E.g. for n=5:

V = {a, b, c, d, e};
E = {{a, b}, {a, c}, {a, d}, {a, e}, {b, c}, {b, d}, {b, e}, {c, d}, {c, e}, {d, e}}.

The full symmetric group $G=S(V) \cong S_n$ then acts on E. Each graph corresponds to a colouring of E by Y = {black, white} and two graphs are isomorphic if and only if they’re isotopic under G – i.e. belong to the same orbit under G. Our objective is to compute the number of unique colourings by applying Polya enumeration theorem.

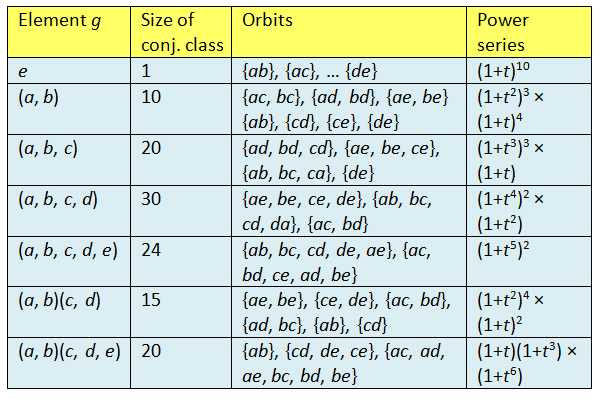
Clearly, c(g) – the number of orbits of g acting on E – only depends on the equivalence class of g in G; in particular for n=5, the number of cases is reduced from 5!=120 to 7.

g=e : c(g) = C(5, 2) = 10;
[10×] g=(a, b): edges ac and bc must share the same colour, as do {ad, bd}, {ae, be}, so c(g) = 7;
[20×] g=(a, b, c): edges ad, bd and cd must have the same colour, as do {ae, be, ce} and {ab, bc, ac}, so c(g) = 4;
[30×] g=(a, b, c, d): edges ae, be, ce and de have the same colour, as do {ab, bc, cd, da} and {ac, bd}, so c(g) = 3;
[24×] g=(a, b, c, d, e): we get two orbits {ab, bc, cd, de, ae} and {ac, bd, ce, ad, be} so c(g)=2;
[15×] g=(a, b)(c, d): we get {ae, be}, {ce, de}, {ac, bd}, {ad, bc}, {ab}, {cd} so c(g)=6;
[20×] g=(a, b)(c, d, e): we get {ab}, {cd, de, ce} and all the remaining edges form a single orbit so c(g)=3.

Hence the number of graphs with 5 vertices, up to isomorphism, is:

$\frac 1 {120} (1\times 2^{10} + 10\times 2^7 + 20\times 2^4 + 30\times 2^3 + 24\times 2^2 + 15\times 2^6 + 20\times 2^3) = 34.$

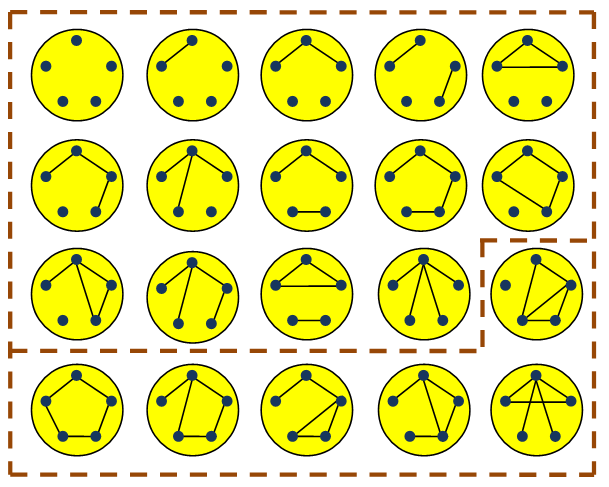
The following diagram lists all isomorphism classes of simple graphs with 5 vertices and up to 5 edges.

Counting Graphs II

In fact, with just a bit more effort, we can compute the number of graphs with 5 vertices and e edges, for each 0 ≤ e ≤ 10. Recall that each graph (ignoring symmetry) is simply a map E → {black, white}. Let X be the set of all such graphs; the group $G\cong S_5$ acts on X by permuting the edges around.

Now, we assign a weight to each colour: black→1 and white→0. Each graph E → {black, white} then gets a weight which is its number of edges. Let X_i be the set of elements in X with weight i; it’s easy to see that $|X_i| = C(10, i)$ .

Our objective is to compute $n_i := |G\backslash X_i|$ , the number of isomorphic classes of simple graphs with 5 vertices and i edges.

To that end, define the polynomial $P(t) := \sum_{i=0}^{10} n_i t^i$ . Burnside’s lemma gives:

$P(t) =\sum_i |G\backslash X_i| t^i = \frac 1 {|G|} \sum_i \sum_{g\in G} |X_i^g|t^i = \frac 1 {|G|}\sum_{g\in G}\left(\sum_i |X_i^g|t^i\right).$

Thus, we need to evaluate the power series $P_g(t) = \sum_i |X_i^g| t^i$ for each g.

g=e : since $X_i^g = X_i$ , this is just $P_g(t) = (1+t)^{10}$ .
g=(a, b) : as worked out earlier, the non-trivial orbits are {ac, bc}, {ad, bd} and {ae, be}. For each of these three orbits, the weight is either 0 or 2, so we get a factor of $(1+t^2)^3$ . For the remaining 4 singleton orbits, we get a factor of $(1+t)^4$ , so the summand is $P_g(t) = (1+t^2)^3 (1+t)^4$ .
g=(a, b, c): the orbits are {de}, {ad, bd, cd}, {ae, be, ce} and {ab, bc, ac}. Each of the three 3-element sets contributes a factor of $(1+t^3)$ while the singleton set contributes (1+t), hence the summand is $(1+t^3)^3(1+t)$ .

Eventually, we get all the seven power series.

Hence, P(t) equals:

$\begin{aligned}\frac 1 {120}(&(1+t)^{10}+10(1+t^2)^3(1+t)^4 + 20(1+t^3)^3(1+t) + 30(1+t^4)^2(1+t^2)\\&+24(1+t^5)^2 + 15(1+t^2)^4(1+t)^2+20(1+t)(1+t^3)(1+t^6)),\end{aligned}$

which gives $1+t+2t^2 + 4t^3+6t^4+6t^5+6t^6 + 4t^7+2t^8+t^9+t^{10}$ . Thus, there are 1 graph with 1 edge, 2 graphs with 2 edges, 4 graphs with 3 edges, … up to isomorphism.

Polya Enumeration Theorem Revisited

Inspired by the above example, we define:

Definition. Let G be a finite group acting on finite set X of size k. Then the cycle index is the polynomial:

$Z_G(t_1, t_2, \ldots, t_k) := \frac 1{|G|}\sum_{g\in G} t_1^{j_1(g)} t_2^{j_2(g)} \ldots t_k^{j_k(g)},$

where $j_c(g)$ is the number of cycles (or orbits) in g of length c.

Examples.

Consider S₃ acting on {1, 2, 3}. Then each term gives:
- g=e : $t_1^3$ ;
- [3×] g=(a, b): $t_1 t_2$ ;
- [2×] g=(a, b, c): $t_3$ , so we have $Z_G(t_1, t_2, t_3) = \frac 1 6(t_1^3 + 3t_1 t_2 + 2t_3)$ .
Consider $G\cong S_5$ acting on the set of edges E earlier. We have:

$Z_G(t_1, t_2, \ldots, t_{10}) = \frac 1 {120}(t_1^{10}+10t_1^4 t_2^3 + 20 t_1 t_3^3 + 30t_2 t_4^2 + 24t_5^2 + 15t_1 t_2^4 + 20t_1 t_3 t_6).$

Now we’re ready to describe a more general form of Polya enumeration theorem. As before, G acts on set X, and we consider the set of all colourings X→Y. But now each colour is endowed with a weight. If we let $X_i$ be the set of colourings with weight i, then our objective is to compute $n_i := |G\backslash X_i|$ via the power series

$P(t) := \sum_{i\ge 0} n_i t^i.$

As worked out before, to do that we need to compute:

$P_g(t) := \sum_{i\ge 0} |X_i^g| t^i$ , for each g in G.

Now if we write g as a product of cycles: g = (cycle 1)(cycle 2) … , where there are $j_c(g)$ cycles of length c, then each cycle must be of uniform colour! In other words, each cycle contributes a term of $(f_0+f_1 t^c + f_2 t^{2c} + f_3 t^{3c}+ \ldots)$ where $f_w$ is the number of colours of weight w. Hence:

$\begin{aligned}P_g(t) = &(f_0+f_1 t + f_2 t^2 +\ldots)^{j_1(g)} (f_0+f_1 t^2 + f_2 t^4+\ldots)^{j_2(g)}\\ &(f_0+f_1 t^3+f_2 t^6+\ldots)^{j_3(g)} \ldots\end{aligned}$

Writing $f(x) = f_0 + f_1 x + f_2 x^2 + \ldots$ , this gives: $P_g(t) = f(t)^{j_1(g)} f(t^2)^{j_2(g)} f(t^3)^{j_3(g)}\ldots$ . Summing up:

$P(t) = \frac 1 {|G|} \sum_{g\in G} P_g(t) = Z_G(f(t), f(t^2), f(t^3), \ldots).$

Let’s summarise all we’ve learnt.

Polya Enumeration Theorem B. Suppose we have $f_w$ colours of weight w and $f(x) := \sum_w f_w x^w$ . Then the number of colourings with a specified weight is given by the generating function:

$P(t) =Z_G(f(t), f(t^2), f(t^3), \ldots)$ .

E.g. in our earlier example of graph counting, we have f(x) = 1+x so the resulting generating function is $P(t) = Z_G(1+t, 1+t^2, 1+t^3, \ldots)$ as we saw above.

Example 1

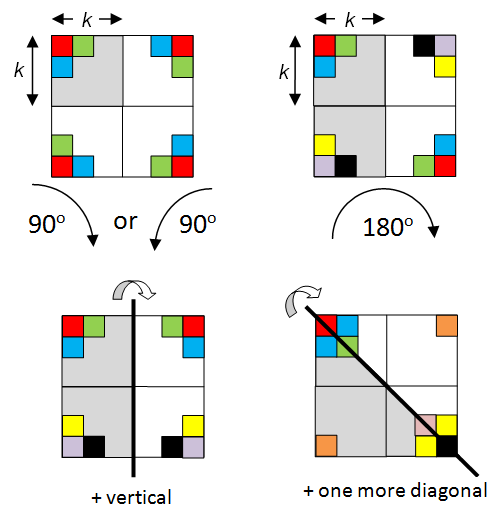
On a 2k × 2k chessboard, each square is to be coloured black or white. Two colourings are identical if they can be obtained from each other by rotation or reflection. Find the generating function for the number of colourings with a specified number of black squares.

Solution

Let’s consider the symmetries of a square.

In the first case, we get k² cycles of length 4 each. In the second and third cases, we get 2k² cycles of length 2 each. In the final case, we get 2k cycles of length 1 and k(2k-1) cycles of length 2. Hence:

$Z_G(t_1, t_2, \ldots) = \frac 1 8 (t_1^{4k^2} + 2t_1^{2k}t_2^{k(2k-1)} + 3t_2^{2k^2} + 2t_4^{k^2}).$

The final answer is thus:

$\begin{aligned}f(t) &= Z_G(1+t, 1+t^2, \ldots)\\&= \frac 1 8 ((1+t)^{4k^2} + 2(1+t)^{2k}(1+t^2)^{k(2k-1)} + 3(1+t^2)^{2k^2} + 2(1+t^4)^{k^2}).\end{aligned}$

Here are some small examples.

k=1: $\begin{aligned} f(t) = t^4+t^3+2t^2+t+1\end{aligned}$ ;
k=2: $\begin{aligned} f(t)=&t^{16}+3t^{15}+21t^{14}+77t^{13}+252t^{12} +567t^{11}+1051 t^{10}+1465 t^9\\&+1674 t^8+1465 t^7+1051 t^6+567 t^5+252 t^4+77 t^3+21 t^2+3 t+1.\end{aligned}$

More generally, we can consider colours with vectorial weights. For example, if each colour has weight (v, w), then we write:

$f(x,y) = \sum_{v,w} f_{v,w} x^v y^w$

where $f_{v,w}$ denotes the number of colours of weight (v, w). Then Polya’s enumeration theorem can be further generalised: the number of colourings with a specified vectorial weight (v, w) is given by the coefficient of $t^v u^w$ in:

$P(t, u) = Z_G(f(t,u), f(t^2, u^2), f(t^3, u^3), \ldots).$

Example 2

Find the number of ways to colour the 12 edges of a cube with {red, green blue} such that each colour occurs on an even number of edges. Two colourings are considered identical if they’re obtained from each other via a rotation.

Solution

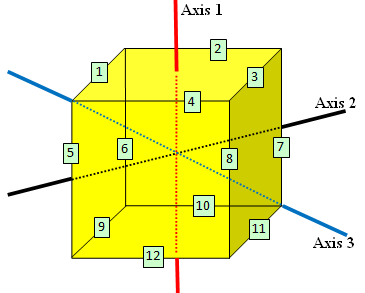
Label the 12 edges of a cube as follows, together with three axes of rotation.

Let’s compute the orbits of the various rotations. There should be 24 rotations in all.

Identity: 12 singleton orbits, {1}, {2}, …, {12}.
[6×] Rotation about axis 1 (90 deg): {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}.
[3×] Rotation about axis 1 (180 deg): {1, 3}, {2, 4}, {5, 7}, {6, 8}, {9, 11}, {10, 12}.
[6×] Rotation about axis 2: {5}, {7}, and 5 orbits of size 2.
[8×] Rotation about axis 3: 4 orbits of size 3.

Hence the cycle index is:

$Z_G(t_1, t_2, \ldots) = \frac 1 {24}(t_1^{12}+6t_4^3 + 3t_2^6+6 t_1^2 t_2^5 + 8t_3^4).$

[ Note: without tracing the exact orbits, we can conclude that the rotation about axis 2 has exactly five orbits of size two. Indeed, since the rotation has order 2, each cycle size is either 1 or 2. The only fixed edges are 5 and 7 so the remaining edges must be paired into five orbits of size two each. ]

We need to compute the number of colourings where green and blue each occurs an even number of times, so assign weight to each colour: red=(0, 0), green=(1, 0) and blue=(0, 1). The weight polynomial is f(x, y) = 1+x+y so the resulting generating function is:

$\begin{aligned} P(t, u)= &\frac 1 {24}[(1+t+u)^{12} + 6(1+t^4+u^4)^3 + 3(1+t^2+u^2)^6\\&+6(1+t+u)^2 (1+t^2+u^2)^5 + 8(1+t^3+u^3)^4].\end{aligned}$

To sum up the coefficients of $t^i u^j$ where i and j are both even, compute the sum

$\frac 1 4(P(1, 1)+P(1,-1)+P(-1,1)+P(-1,-1))=5823$ . ♦

The Case of Full Symmetric Group

Suppose |X|=k and |Y|=n and G is the full symmetric group $S(X) \cong S_k$ . In the previous article, considering this group led us to the formulation of Stirling numbers. Let’s consider the case of the cycle index:

$Z_G(t_1, t_2, \ldots) = \sum_{g\in S_k} t_1^{j_1(g)} t_2^{j_2(g)}\ldots.$

What can we say about this power series?

To answer them, let’s assign some weights to the n colours. To distinguish all the n distinct colours, we’ll assign an (n-component) vectorial weight:

colour 1 ↔ (1, 0, …, 0), colour 2 ↔ (0, 1, …, 0), … …, colour n ↔ (0, 0, …, 1).

Hence, the weight of a colouring tells us the number of occurrences of each colour. The corresponding weight polynomial is then a linear function in n variables:

$f(x_1, x_2, \ldots, x_n) = x_1 + x_2 + \ldots + x_n.$

Applying the multivariate version of the Polya enumeration theorem, we see that the number of colourings of a specified weight $(w_1, w_2, \ldots, w_n)$ is given by the generating function:

$Z_G(f(u_1, u_2, \ldots, u_n), f(u_1^2, u_2^2, \ldots, u_n^2), \ldots) = Z_G(p_1, p_2, p_3, \ldots),$

where $p_i = u_1^i + u_2^i + \ldots + u_n^i$ is the i-th power symmetric function. The question is: how many colourings are of weight $(w_1, w_2, \ldots, w_n)$ , up to symmetry? Since we have the full symmetric group acting on X, the answer is obvious: 1 if $\sum_i w_i = k$ and 0 otherwise. Now if we multiply this by an auxiliary $t^k$ and sum over all k=|X|, we get the resulting power series:

$\begin{aligned}\sum_{k=0}^\infty Z_{S_k}(p_1, p_2, p_3, \ldots) t^k &= \sum_{w_1, \ldots,w_n\ge 0} u_1^{w_1} u_2^{w_2}\ldots u_n^{w_n}\cdot t^{\sum w_i}\\&= \frac 1 {1-u_1t}\cdot \frac 1{1-u_2t}\cdot\dots \cdot \frac 1 {1-u_n t}.\end{aligned}$

Writing each term

$(1-u_i t)^{-1} = \exp(\log(1-u_i t)) = \exp\left(u_i t + \frac {u_i^2 t^2} 2 + \frac{u_i^3 t^3} 3 + \ldots\right),$

we get the final result:

$\begin{aligned}\sum_{k=0}^\infty Z_{S_k}(p_1, p_2, \ldots)t^k = \exp\left(p_1 t + \frac {p_2} 2 t^2 + \frac {p_3} 3 t^3 + \ldots\right).\end{aligned}$

Example

To compute the cycle index for $G=S_5$ , let $T = p_1 t + \frac {p_2} 2 t^2 + \frac{p_3}3 t^3 + \ldots$ . We need to compute the expansion of exp(T) until T⁵ and find the coefficient of t⁵.

$T : p_5/5$ ;
$T^2 : p_1 p_4/2 + p_2 p_3/3$ ;
$T^3 : p_1^2 p_3 + 3p_1 p_2^2/4$ ;
$T^4 : 2p_1^3 p_2$ ;
$T^5 : p_1^5$ .

Hence, the final sum is

$\begin{aligned}&\frac{p_5}5 + \frac 1 {2!}\left(\frac{p_1 p_4}2 + \frac{p_2 p_3}3\right) + \frac 1 {3!}\left(p_1^2 p_3 + \frac {3 p_1 p_2^2}4\right) + \frac 1 {4!}\left(2p_1^3 p_2\right) + \frac 1 {5!}p_1^5 \\= &\frac 1 {120}\left(24p_5 + 30p_1p_4 + 20p_2p_3 + 20p_1^2 p_3 + 15 p_1 p_2^2 +10p_1^3 p_2 + p_1^5\right).\end{aligned}$

In conclusion, in the group $S_5$ , there are:

1 identity element,
24 elements of type (a, b, c, d, e),
30 elements of type (a, b, c, d),
20 elements of type (a, b)(c, d, e),
20 elements of type (a, b, c),
15 elements of type (a, b)(c, d), and
10 elements of type (a, b).

All these were obtained via generating functions.

Leave a Reply Cancel reply

Recent Posts

Archives

Categories

Meta

Pages