Polynomials and Representations XXIII

Posted on June 3, 2016 by limsup

Power-Sum Polynomials

We will describe how the character table of S_d is related to the expansion of the power-sum symmetric polynomials in terms of monomials. Recall:

\displaystyle p_k = x_1^k + x_2^k + \ldots, \qquad p_\lambda = p_{\lambda_1} p_{\lambda_2} \ldots p_{\lambda_l},

where l =l(\lambda) exactly since p_0 is not defined.

Now each irrep of S_d is of the form V_\mu for some \mu\vdash d; we will denote its character by \chi_\mu. Each conjugancy class of S_d is also given by [g_\lambda] where \lambda\vdash d and g_\lambda \in S_d has cycle structure \lambda. E.g. if \lambda = (4,2,1) we can take g_\lambda = (2,4,6,7)(1,3) \in S_7 as a representative.

We will calculate the character value \chi_\mu(g_\lambda) by looking at the characters of U_\mu = \mathbb{C}[X_\mu]. For that, we need:

Lemma. If the finite group G acts on finite set X, then the trace of g : \mathbb{C}[X] \to \mathbb{C}[X] is: |\{x \in X : gx = x\}|, the number of fixed points of g in X.

Proof

Taking elements of X as a natural basis of \mathbb{C}[X], the matrix representing g\in G is a permutation matrix. Its trace is thus the number of ones along the main diagonal, which is the number of fixed points of g\in G. ♦

Hence we have:

Theorem. Let P_{\lambda\mu} be the trace of g_\lambda on U_\mu = \mathbb{C}[X_\mu]. Expressing each p_\lambda as a sum of monomials, we get:

\displaystyle p_\lambda = \sum_\mu P_{\lambda\mu} m_\mu.

Proof

Let us compute the coefficient of x^\mu in the expansion of p_\lambda = p_{\lambda_1}\ldots p_{\lambda_l}. For illustration let us take \lambda = (3, 2, 2, 1, 1) and \mu = (4, 3, 2); pick the representative g_\lambda =(1, 2, 3)(4, 5)(6, 7)(8)(9). To obtain terms with product x_1^4 x_3^3 x_2^2, here is one possibility:

\begin{aligned}p_3 &= \boxed{x_1^3} + x_2^3 + x_3^3 + \ldots\\p_2 &= x_1^2 + \boxed{x_2^2} + x_3^2 + \ldots\\ p_2 &= x_1^2 + x_2^2 + \boxed{x_3^2} + \ldots\\ p_1 &= x_1 + \boxed{x_2} + x_3 + \ldots\\ p_1 &= \boxed{x_1} + x_2 + x_3 + \ldots\end{aligned} \implies \begin{array}{|c|c|c|}\hline\{1, 2, 3\} &  &\\ & \{4, 5\} & \\ & & \{6, 7\}\\ & \{8\} & \\ \{9\}& & \\ \hline\end{array}

The corresponding fixed point (A_1, A_2, A_3) \in X_\mu is given by A_1 = \{1, 2, 3, 9\}, A_2 = \{4, 5, 8\} and A_3 = \{6, 7\}.

In the general case, each contribution of x^\mu corresponds to a selection of: 1 \le i_1, i_2, \ldots, i_m \le l(\mu) such that

x_{i_1}^{\lambda_1} \cdot x_{i_2}^{\lambda_2} \cdot \ldots \cdot x_{i_m}^{\lambda_m} = x^\mu.

This corresponds to a partition [d] = \coprod_i A_i, defined by running through all the cycles of g_\lambda and putting the elements of the c-th cycle into the set A_{i_c} for 1 \le c \le m. Such a partition is invariant under g_\mu. ♦

blue-lin

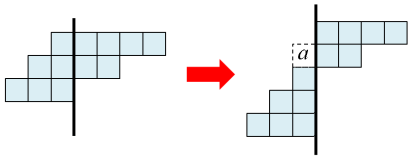
Example

Thus P_{\lambda\mu} is the number of ways of “merging” terms \lambda_i to form the partition \mu upon sorting. For example, taking \lambda = (3,2,2,1,1) and \mu = (4,3,2) from above, the coefficient of x_1^4 x_2^3 x_3^2 in p_\lambda is 7:

power_sum_symmetric_expansion

Character Table

Writing the above vectorially, we have \mathbf{p} = \mathbf P \cdot \mathbf m, where \mathbf P = (P_{\lambda\mu}) is the trace of g_\lambda on U_\mu = \oplus_{\nu}V_\nu^{K_{\nu\mu}}. Thus, we have

\displaystyle P_{\lambda\mu} = \sum_{\nu} K_{\nu\mu} \text{tr}(g_\lambda : V_\nu \to V_\nu)

which gives us \mathbf P = \mathbf X\cdot \mathbf K where \mathbf X_{\lambda\mu} = \text{tr}(g_\lambda : V_\mu \to V_\mu) so X is the transpose of the character table for S_d. Hence, we have:

\mathbf p = \mathbf X\mathbf K\mathbf m= \mathbf X\cdot\mathbf s.

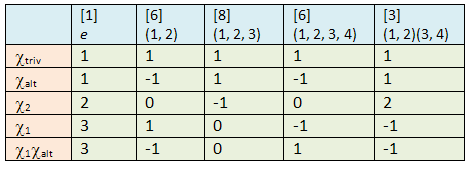
Example: S4

For d=4 we obtain:

\mathbf P = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 2 & 0 & 0 \\ 1 & 2 & 2 & 2 & 0 \\1 & 4 & 6 & 12 & 24\end{pmatrix}, \quad \mathbf K = \begin{pmatrix}1 &1 &1 & 1 & 1\\ 0 & 1 & 1 & 2 & 3 \\ 0 & 0 & 1 & 1 & 2 \\ 0 & 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 0 & 1\end{pmatrix}\implies \mathbf X= \begin{pmatrix} 1 & -1 & 0 & 1 & -1\\ 1 & 0 & -1 & 0 & 1\\ 1 & -1 & 2 & -1 & 1 \\ 1 & 1 & 0 & -1& -1 \\ 1 & 3 & 2 & 3 & 1\end{pmatrix}

where the rows and columns are indexed by partitions 4, 31, 22, 211 and 1111. One checks that \mathbf X^t is the character table for S_4:

chartable_s4_2

Orthogonality

Finally, orthonormality of irreducible characters translates to orthogonality of power-sum polynomials.

Proposition. The polynomials p_\lambda form an orthogonal set, and \left<p_\lambda, p_\lambda\right> = z_\lambda is the order of the centralizer of any g_\lambda with cycle structure \lambda.

Proof

Since p_\lambda = X_{\lambda\mu} s_\mu and the s_\mu are orthonormal,

\displaystyle\left< p_\lambda, p_{\lambda'}\right> = \sum_\mu X_{\lambda\mu} X_{\lambda'\mu},

which is entry (\lambda, \lambda') of \mathbf X \mathbf X^t. This is the dot product between columns \lambda and \lambda' of the character table. By standard character theory, it is \delta_{\lambda\lambda'} \frac{|G|} {|C_\lambda|} where C_\lambda is the conjugancy class containing g_\lambda. Now apply \frac{|G|}{|C_\lambda|} = z_\lambda. ♦

Under the Frobenius map, the power-sum symmetric polynomial corresponds to:

p_\lambda = \sum_\mu X_{\lambda\mu} s_\mu\ \mapsto\ \sum_\mu \chi_\mu(g_\lambda) \chi_\mu,

so p_\lambda(g) = \begin{cases} z_\lambda, &\text{if } g \text{ has cycle structure }\lambda, \\ 0, &\text{otherwise.}\end{cases}

blue-lin

Posted in Uncategorized | Tagged , , , , | Leave a comment

Polynomials and Representations XXII

Posted on June 1, 2016 by limsup

Product of Representations

Recall that the Frobenius map gives an isomorphism of abelian groups:

correspondence_polynomial_and_character

Let us compute what the product \Lambda^{(d)} \times \Lambda^{(e)} \to \Lambda^{(d+e)} corresponds to on the RHS.

For that, we take h_\lambda \in \Lambda^{(d)} and h_\mu \in \Lambda^{(e)} where \lambda\vdash d and \mu\vdash e. Multiplication gives h_\lambda h_\mu = h_{\lambda | \mu} where \lambda|\mu is the partition obtained by sorting (\lambda_1, \lambda_2, \ldots, \mu_1, \mu_2, \ldots). Next, we use the following standard result.

Lemma. Let G act transitively on non-empty set X. Pick any x_0 \in X and let H = \{g\in G : gx_0 = x_0\} be its stabiliser. Then:

\mathbb{C}[X] \cong \text{Ind}_H^G \mathbb{C},

the trivial module on H induced to G.

Proof

The RHS is \mathbb{C}[G] \otimes_{\mathbb{C}[H]} \mathbb{C} by definition. Now we map gx_0\in X on the LHS to g\otimes 1 on the RHS. Now:

gx_0 = g'x_0 \iff g^{-1}g' \in H \iff g^{-1}g' \otimes 1 = 1\otimes 1 \iff g\otimes 1 = g'\otimes 1.

Since the action on X is transitive, this gives an isomorphism of vector spaces, which clearly commutes with the group action. ♦

In particular U_\lambda = \mathbb{C}[X_\lambda] is isomorphic to \text{Ind}_H^G \mathbb{C} where G = S_d and H is the stabiliser group of any partition of [d] into disjoint sets of sizes \lambda_i. Clearly H is isomorphic to the product \prod_i S_{\lambda_i} so we have:

\displaystyle U_\lambda \cong \text{Ind}_{S_{\lambda_1} \times S_{\lambda_2}\times \ldots}^{S_d}\, \mathbb{C},\quad U_\mu \cong \text{Ind}_{S_{\mu_1} \times S_{\mu_2}\times \ldots}^{S_e}\, \mathbb{C},

\displaystyle U_{\lambda |\mu} \cong \text{Ind}_{S_{\lambda_1} \times S_{\lambda_2} \times\ldots \times S_{\mu_1} \times S_{\mu_2}\times\ldots}^{S_{d+e}} \,\mathbb{C}.

Proposition. The product \Lambda^{(d)} \times \Lambda^{(e)} \to \Lambda^{(d+e)} corresponds to:

(V, W) \mapsto \text{Ind}_{S_d \times S_e}^{S_{d+e}} V \otimes W

where S_d \times S_e acts on V\otimes W via (g,h) : v\otimes w\mapsto (gv)\otimes (hw).

Proof

First use the following result, whose proof is an easy exercise if you know tensor products (here, tensor products without subscripts are over C).

  • Suppose B, B' are \mathbb{C}-algebras, A\subseteq B, A'\subseteq B' are subalgebras, and V, W are A, A'-modules respectively. Then (B \otimes_{A} V) \otimes (B'\otimes_{A'} W) \cong (B\otimes B') \otimes_{A \otimes A'} (V\otimes W).

In particular, take

B=\mathbb{C}[G],\quad B' = \mathbb{C}[G'],\quad A=\mathbb{C}[H],\quad A'=\mathbb{C}[H']

for subgroups H'\le G' and H\le G. Since \mathbb{C}[G\times G'] \cong \mathbb{C}[G]\otimes \mathbb{C}[G'] as \mathbb{C}-algebras, we have:

\left(\text{Ind}_H^G V\right) \otimes \left( \text{Ind}_{H'}^{G'} W\right) \cong \text{Ind}_{H\times H'}^{G\times G'} V\otimes W.

This gives U_\lambda \otimes U_\mu \cong \text{Ind}_{S_{\lambda_1} \times \ldots \times S_{\mu_1} \times \ldots }^{S_d \times S_e} \mathbb{C}. So we have:

\text{Ind}_{S_d\times S_e}^{S_{d+e}} (U_\lambda \otimes U_\mu) \cong U_{\lambda | \mu},

corresponding to h_\lambda h_\mu = h_{\lambda|\mu} as desired. ♦

blue-lin

Consequences

Ring Isomorphism

Thus we obtain a graded ring isomorphism between \Lambda and the set of virtual representations of all S_d up to isomorphism. And we have:

\displaystyle s_\mu s_\nu = \sum_\lambda c^{\lambda}_{\mu\nu} s_\lambda \implies \text{Ind}_{S_d \times S_e}^{S_{d+e}} (V_\mu \otimes V_\nu) = \bigoplus_\lambda V_\lambda^{\oplus c^{\lambda}_{\mu\nu}}.

Pieri’s Formulae

Consider the case where W is trivial and e=1, so the product operation gives

V \mapsto \text{Ind}_{S_d}^{S_{d+1}}\, V.

On the other hand the trivial representation for S_1 corresponds to h_1 = e_1 \in \Lambda^{(1)}. By Pieri’s formula, h_1 s_\lambda = \sum_\mu s_\mu where \mu runs through all partitions obtained from \lambda by adding 1 box. Hence:

\displaystyle \text{Ind}_{S_d}^{S_{d+1}} V_\lambda = \bigoplus_\mu V_\mu.

For example,

\text{Ind}_{S_{14}}^{S_{15}} V_{533111} \cong V_{633111} \oplus V_{543111} \oplus V_{533211} \oplus V_{5331111}.

Restriction

By Frobenius reciprocity, we have, for any \lambda \vdash d and \nu \vdash d+ 1,

\left< V_\lambda, \text{Res}_{S_{d+1}}^{S_d} V_\nu\right> = \left< \text{Ind}_{S_d}^{S_{d+1}} V_\lambda, V_\nu\right> = \begin{cases} 1, \quad &\text{if } \nu \text{ is obtained from } \lambda \text{ by adding 1 box,}\\0, \quad &\text{else.}\end{cases}.

Hence, \text{Res}_{S_{d+1}}^{S_d} V_\nu = \oplus_\lambda V_\lambda where the sum is over all partitions \lambda obtained from \nu by removing one box.

Exercise

Express \text{Res}_{S_{17}}^{S_{15}} V_\lambda and \text{Ind}_{S_{17}}^{S_{19}} V_\lambda as a direct sums of irreps where \lambda = (6,3,3,3,1,1).

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

Polynomials and Representations XXI

Posted on May 30, 2016 by limsup

We have established that all irreps of S_d are defined over \mathbb{Q} and hence any field of characteristic 0. For convenience we will fix K = \mathbb{C}.

Twists

For any group G and representation \rho : G \to \text{GL}(V) over \mathbb{C}, if \chi : G \to \mathbb{C}^* is a group homomorphism, we can twist \rho as follows:

\rho \otimes \chi : G\to \text{GL}(V), \qquad g \mapsto \rho(g)\chi(g).

Sometimes, we also write V\otimes\chi for the twist; this gives an action on the set of all irreducible representations of G. Note that \dim(V\otimes\chi) = \dim(V) so the dimension of V is invariant among the equivalence classes of twists.

For example in S_4, the character table is:

chartable_s4_2

so we have 3 equivalence classes of irreps if we twist by \chi_{\text{alt}}.

blue-lin

Symmetric Group

When G = S_d, we let \chi be the alternating character, i.e. \chi(g) := \text{sgn}(g) \in \{+1, -1\}. Now we consider the modules U_\lambda \otimes \chi = \mathbb{C}[X_\lambda] \otimes \chi.

Question. What is the following:

\left< U_\mu, U_\lambda \otimes \chi\right> = \dim_{\mathbb{C}} \text{Hom}_{\mathbb{C}[G]}(U_\mu, U_\lambda \otimes\chi)?

Answer

Note that the underlying vector space for U_\lambda \otimes\chi is the same as U_\lambda though the action has a twist. Recall that, as G-modules,

\text{Hom}_\mathbb{C}(U_\mu, U_\lambda \otimes \chi) \cong \mathbb{C}[X_\mu] \otimes \mathbb{C}[X_\lambda] \otimes \chi\cong \mathbb{C}[X_\mu \times X_\lambda] \otimes \chi

and we wish to find all G-invariant elements in this space.

Each element \alpha on the RHS is a linear combination of elements ((A_i), (B_j)) \in X_\mu \times X_\lambda. Let us unwind the definition for \alpha to be invariant under G. Note that:

[d] = A_1 \coprod \ldots \coprod A_l = B_1 \coprod \ldots \coprod B_m, \qquad |A_i| = \mu_i, |B_j| = \lambda_j

and g\in S_n takes it to \chi(g) \cdot (g(A_i), g(B_j)). Now if any A_i \cap B_j has more than one element, then the transposition g\in S_d which swaps them would flip the sign while leaving g(A_i) = A_i, g(B_j) = B_j. Thus we have shown:

  • If |A_i \cap B_j| \ge 2 for some i, j, then the coefficient of ((A_i), (B_j)) in \alpha is zero.

Conversely, if |A_i \cap B_j| \le 1 for all i, j, then no g\in S_d takes ((A_i), (B_j)) back to itself, so as it ranges over an orbit, the coefficient of ((A_i), (B_j)) in \alpha is uniquely determined.

Example

Suppose d=3 and \lambda = \mu = (2,1) so we get

[3] = \overbrace{\{2,3\}}^{A_1} \cup \overbrace{\{1\}}^{B_1} = \overbrace{ \{1,3\} }^{A_2} \cup \overbrace{\{2\}}^{B_2} = \overbrace{ \{1,2\} }^{A_3} \cup \overbrace{ \{3\}}^{B_3}.

Then X_\lambda \times X_\mu has 9 elements (A_i, B_i, A_j, B_j) for 1\le i,j\le 3. Any invariant element in \mathbb{C}[X_\mu \times X_\lambda]\otimes \chi must be a multiple of:

\begin{aligned} &(A_1, B_1,A_2, B_2) - (A_1, B_1, A_3, B_3) - (A_2, B_2, A_1, B_1) \\- &(A_3, B_3, A_2, B_2) + (A_2, B_2, A_3, B_3) + (A_3, B_3, A_1, B_1).\end{aligned}

Conclusion. We have:

\left<U_\mu, U_\lambda\otimes \chi\right> = \text{Hom}_{\mathbb{C}[G]}(U_\mu, U_\lambda \otimes \chi) = N_{\lambda\mu},

the number of binary matrices a_{ij} such that \sum_i a_{ij} = \lambda_j and \sum_j a_{ij} = \mu_i.

blue-lin

Consequences

We saw that \mathbf N = (N_{\lambda\mu}) satisfies:

\mathbf N = \mathbf K^t \mathbf J \mathbf K,

where J is the permutation matrix which swaps \lambda with its transpose \overline \lambda. Writing U_\mu = \oplus_{\nu} V_\nu^{\oplus K_{\nu\mu}} we get:

\displaystyle N_{\mu\lambda} = N_{\lambda\mu} = \sum_\nu K_{\nu\mu}\left<V_\nu, U_\lambda\otimes\chi\right>.

If A_{\nu\lambda} = \left<V_\nu, U_\lambda\otimes\chi\right> then writing in matrix form gives \mathbf K^t \mathbf A = \mathbf N. Hence \mathbf A = \mathbf J\mathbf K and we have \left<V_\nu, U_\lambda\otimes\chi\right> = K_{\overline\nu\lambda}. Thus:

\displaystyle \bigoplus_\nu (V_\nu \otimes\chi)^{\oplus K_{\nu\lambda}}= U_\lambda\otimes\chi = \bigoplus_\nu V_\nu^{\oplus K_{\overline\nu \lambda}} = \bigoplus_\nu V_{\overline\nu} ^{\oplus K_{\nu\lambda}}.

Since the matrix K_{\nu\lambda} is invertible we have proven:

Proposition. V_\lambda\otimes \chi \cong V_{\overline\lambda}.

In particular, V_\lambda\otimes\chi \cong V_\lambda if and only if \lambda is its own transpose, e.g. (5, 3, 2, 1, 1).

Hence under the Frobenius map, the corresponding symmetric polynomial for U_\lambda\otimes\chi is \sum_\nu K_{\overline\nu \lambda}s_\nu = e_\lambda.

Also, the involution \omega : \Lambda^{(d)} \to \Lambda^{(d)} which maps e_\lambda \leftrightarrow h_\lambda corresponds to V \leftrightarrow V\otimes\chi. This gives an algebraic interpretation for \omega.

Posted in Uncategorized | Tagged , , , , | Leave a comment

Polynomials and Representations XX

Posted on May 28, 2016 by limsup

From now onwards, we will assume the base field K has characteristic 0.

Example: d=3

Following the previous article, we examine the case of S_3. We get 3 partitions: \lambda_1 = (3), \lambda_2 = (2,1) and \lambda_3 = (1,1,1). Let us compute M_{ij} := \left < U_{\l_i}, U_{\l_j}\right> for all 1 \le i, j \le 3. From the previous article, we have:

modules_for_s3

Since \left< U_{\lambda_1}, U_{\lambda_1}\right> = 1, U_{\lambda_1} is absolutely irreducible (i.e. irreducible even over the algebraic closure of K). Since

\displaystyle \left< U_{\lambda_2}, U_{\lambda_1} \right> = \left< U_{\lambda_3}, U_{\lambda_1}\right> = 1

each of U_{\lambda_2} and U_{\lambda_3} contains exactly one copy of U_{\lambda_1}. Thus we write

\displaystyle U_{\lambda_2} = U_{\lambda_1} \oplus U'_{\lambda_2}, \quad U_{\lambda_3} = U_{\lambda_1} \oplus U'_{\lambda_3},

where U'_{\lambda_i} does not contain U_{\lambda_1}, i.e. \left< U_{\lambda_1}, U'_{\lambda_i}\right> = 0. Hence

\displaystyle \left< U_{\lambda_2}, U_{\lambda_2}\right> = \left< U_{\lambda_1}, U_{\lambda_1}\right>+ \left< U'_{\lambda_2}, U'_{\lambda_2}\right> \implies \left< U'_{\lambda_2}, U'_{\lambda_2}\right> = 1.

Taking \left< U'_{\lambda_i}, U'_{\lambda_j}\right>, we obtain:

modules_for_s3_r2

Thus \left< U'_{\lambda_2}, U'_{\lambda_2}\right> = 1 so U'_{\lambda_2} is absolutely irreducible. Since \left< U'_{\lambda_2}, U'_{\lambda_3}\right> = 2, U'_{\lambda_3} contains two copies of U'_{\lambda_2}. Thus we write:

U'_{\lambda_3}=(U'_{\lambda_2})^{\oplus 2}\oplus U''_{\lambda_3},

where U''_{\lambda_3} does not contain U_{\lambda_1} or U'_{\lambda_2}. We have

\displaystyle 5 = \left< U'_{\lambda_3}, U'_{\lambda_3}\right> = 4\left< U'_{\lambda_2}, U'_{\lambda_2}\right> +\left< U''_{\lambda_3}, U''_{\lambda_3}\right> \implies \left< U''_{\lambda_3}, U''_{\lambda_3}\right> = 1.

Since S_3 has 3 irreducible representations, we have found all of them: U_{\lambda_1}, U'_{\lambda_2}, U''_{\lambda_3} and:

\begin{aligned}U_{\lambda_1} &= U_{\lambda_1}, \\ U_{\lambda_2} &= U_{\lambda_1} \oplus U'_{\lambda_2}, \\ U_{\lambda_3} &= U_{\lambda_1} \oplus (U'_{\lambda_2})^{\oplus 2} \oplus U''_{\lambda_3}.\end{aligned}

Furthermore, we have shown that the 3 irreps of S_3 are in fact defined over \mathbb{Q}.

blue-lin

General Case

We will show that the above computations can be generalised to any S_n. Indeed, the representations U_\lambda := K[X_\lambda] satisfy:

\displaystyle \left< U_\lambda, U_\mu \right> = M_{\lambda\mu}.

Recall that the matrix \mathbf M = (M_{\lambda\mu}) satisfies \mathbf M = \mathbf K^t \mathbf K where K_{\lambda\mu} is the number of SSYT of shape \lambda and type \mu and we have:

  1. K_{\lambda\lambda} = 1 for all \lambda;
  2. if K_{\mu\lambda} \ne 0, then \mu \trianglerighteq \lambda and so \mu \ge \lambda lexicographically.

Thus: M_{\lambda\mu} = \sum_{\nu \trianglerighteq\lambda,\, \nu\trianglerighteq\mu} K_{\nu\lambda} K_{\nu\mu}.

blue-lin

Theorem. Suppose (\Sigma, \le) is a finite partially ordered set and \{U_\lambda\}_{\lambda\in\Sigma} is a collection of representations. And suppose there are non-negative integers \{K_{\lambda\mu}\}_{\lambda, \mu\in\Sigma} satisfying K_{\lambda\lambda} = 1 and:

\displaystyle \left< U_\lambda, U_\mu\right> = \sum_{\nu\ge \lambda, \nu\ge \mu} K_{\nu\lambda} K_{\nu\mu}.

Then there are non-isomorphic absolutely irreducible \{V_\lambda\}_{\lambda\in\Sigma} defined over K such that:

U_\lambda = \bigoplus_{\mu\ge\lambda} V_\mu^{\oplus K_{\mu\lambda}}.

Proof

Choose a maximal element \lambda\in \Sigma; then

\left< U_\lambda, U_\lambda\right> = \sum_{\nu\ge\lambda} K_{\nu\lambda}^2 = K_{\lambda\lambda}^2 = 1.

So V_\lambda := U_\lambda is absolutely irreducible. The number of copies of V_\lambda contained in each U_\mu is:

\left< U_\mu, U_\lambda\right> = \sum_{\nu\ge \lambda,\, \nu\ge \mu} K_{\nu\lambda} K_{\nu\mu} =K_{\lambda\lambda} K_{\lambda\mu} = K_{\lambda\mu}.

so we can write: U_\mu = V_\lambda^{\oplus K_{\lambda\mu}} \oplus U_\mu' where U_\mu' does not contain V_\lambda. This then gives us:

\displaystyle\begin{aligned}\left < U_\mu', U_\nu'\right> = \left < U_\mu, U_\nu\right> - K_{\lambda\mu} K_{\lambda\nu} = \sum_{\substack{\lambda' \ne \lambda, \\ \lambda' \ge \mu,\ \lambda' \ge \nu}} K_{\lambda'\mu} K_{\lambda'\nu}\end{aligned}

so the collection of U_\mu' for \mu \in \Sigma - \{\lambda\} with K_{\mu\nu} satisfy the given conditions and we may proceed recursively with this reduced set. ♦

Applying the above theorem to the set \Sigma = \{\lambda: \lambda\vdash d\} and the representations U_\lambda of S_d, we get:

Corollary. There are absolutely irreducible representations \{V_\lambda\}_{\lambda\vdash d} of S_d defined over \mathbb{Q} such that:

\displaystyle U_\lambda = \bigoplus_{\mu\trianglerighteq \lambda} V_\mu^{\oplus K_{\mu\lambda}}.

blue-lin

Consequences

If we apply this to the case d=3, we get irreps V_3, V_{21}, V_{111} such that:

U_3 = V_3, \qquad U_{21} = V_{21} \oplus V_3, \qquad U_{111} = V_{111} \oplus V_{21}^{\oplus 2} \oplus V_3

as we had computed earlier.

Note 1

Recall that f_\lambda is the number of SYT of shape \lambda, i.e. f_\lambda = K_{\lambda\mu} where \mu = (1,1,\ldots,1). Now U_\mu is the regular representation and K_{\lambda\mu} is the number of copies of V_\lambda contained in it. From character theory we thus have

Note 2: Frobenius Map

If we let \chi_\lambda be the character for the irrep V_\lambda, then:

\chi(U_\lambda) = \sum_{\mu} K_{\mu\lambda} \chi_\mu \implies \vec\chi_U = \mathbf K^t \vec \chi

where the second equation is the vectorial form of the first.

Hence, if each U_\lambda corresponds to the complete symmetric polynomial h_\lambda \in \Lambda^{(d)}, then V_\lambda corresponds to the Schur polynomial s_\lambda and the Hall inner product \Lambda^{(d)}\times \Lambda^{(d)} \to \mathbb{Z} corresponds to (V, W) \mapsto \dim_K \text{Hom}_{K[G]}(V, W).

Thus we have a group isomorphism between \Lambda^{(d)} and the group of virtual characters of S_d, called the Frobenius characteristic map. [Recall that virtual characters are formal differences of the form \chi_1 - \chi_2 where \chi_1, \chi_2 are group characters. The set of virtual characters of a finite group G forms a ring R(G), under addition and multiplication of characters as functions. R(G) is a finitely generated free abelian group, with a basis given by the irreps of G.]

Taken over the rational field, we obtain a linear isomorphism between:

  • \Lambda^{(d)} \otimes_{\mathbb Z} \mathbb Q, the space of symmetric polynomials of degree d with rational coefficients;
  • the space of class functions S_d \to \mathbb{Q}.

blue-lin

Posted in Uncategorized | Tagged , , , , , | Leave a comment

Polynomials and Representations XIX

Posted on May 26, 2016 by limsup

Representations of the Symmetric Group

Let [d] be the set {1,…,d}, and Sd be the group of bijections g: [d] \to [d]. From here on, we shall look at the representations of S_d. Note that this requires a good understanding of representation theory (character theory) of finite groups.

To start, let us first find some representations.

Definition. Given a partition \lambda \vdash d, let X_\lambda be the set of partitions of [d] into disjoint subsets A_1 \coprod \ldots \coprod A_l such that |A_i| =\lambda_i for each i. The group G = S_d then acts on X_\lambda via:

(A_1, A_2, \ldots, A_l) \overset {g \in S_d} \mapsto  (g(A_1), g(A_2), \ldots, g(A_l)).

Note

If \lambda_i = \lambda_{i+1}, the partitioning is considered different when we swap A_i and A_{i+1}. For example if d = 4 and \lambda = (2, 2), then X_\lambda has 6 elements:

\begin{aligned}( \{1,2\}, \{3,4\}), \quad (\{1,3\}, \{2,4\}), \quad (\{1,4\}, \{2,3\}), \\ (\{2,3\}, \{1,4\}), \quad (\{2,4\}, \{1,3\}), \quad (\{3,4\}, \{1,2\}).\end{aligned}

In general,

\displaystyle |X_\lambda| = \frac {d!} {\lambda_1 ! \lambda_2 ! \ldots \lambda_l !}.

As X_\lambda is a G-set, we see that U_\lambda := K[X_\lambda] is a K[G]-module for any field K. Two special cases are of interest.

  • \lambda = (d): X has a single element so U_\lambda is the trivial representation;
  • \lambda = (1,1,\ldots): X is just the set of permutations of [d] so U_\lambda is the regular representation.

Exercise

Show that for \lambda = (d-1, 1), U_\lambda is the standard representation of S_d on [d].

Let us study such representations in a more general setting.

blue-lin

Representations From G-Sets

Let G be a group and X a G-set; then K[X] is naturally a K[G]-module. We then have the following isomorphisms of K[G]-modules:

Lemma.

  • K[X]^\vee \cong K[X] (i.e. K[X] is isomorphic to its dual);
  • K[X] \otimes_K K[Y] \cong K[X\times Y];
  • \text{Hom}_K(K[X], K[Y]) \cong K[X\times Y];
  • K[X]^G = \{v\in K[X] : \forall g\in G, gv = v\} has dimension |G\backslash X|, the number of orbits of X.

Note

In general, a representation is not isomorphic to its dual.

Proof

Take the bilinear map K[X] \times K[X] \to K induced linearly from the map:

X \times X\to K, \quad (x, y) \mapsto \delta_{xy} = \begin{cases} 1, \quad &\text{if } x=y,\\ 0,\quad &\text{if } x\ne y.\end{cases}

This induces an isomorphism K[X] \to K[X]^\vee of vector spaces. It is also G-equivariant since the bilinear map is G-equivariant, which proves the first statement.

For the second, linear algebra gives K[X]\otimes_K K[Y] \cong K[X \times Y] as vector spaces, taking x\otimes y \mapsto (x, y). One easily checks that it is G-equivariant.

The third statement follows from the first two since generically, we have \text{Hom}(V, W) \cong V^\vee \otimes_K W for any K[G]-modules V and W. Thus:

\text{Hom}_K(K[X], K[Y]) \cong K[X]^\vee \otimes_K K[Y] \cong K[X] \otimes_K K[Y] \cong K[X\times Y].

Finally, if \sum_{x\in X} c_x x\in K[X] is invariant under every g\in G, then c_x = c_{g x} for all g\in G and x\in X. Thus c_x is constant when x\in X runs through an orbit. ♦

blue-lin

Now assume that char(K) = 0.

Question. Given \lambda, \mu \vdash d, what is the following value:

\displaystyle \left<U_\mu, U_\lambda\right>_G = \dim_L\text{Hom}_{L[G]}(L[X_\mu], L[X_\lambda])

where L is the algebraic closure of K?

Note

The reader may assume K =\mathbb{C} to simplify matters, in which case L = K and when we mention “absolutely irreducible”, just replace it with “irreducible”.

Answer

By the above lemma, we have:

\text{Hom}_{K[G]} (K[X_\mu], K[X_\lambda]) =\text{Hom}_K (K[X_\mu], K[X_\lambda])^G \cong K[X_\lambda \times X_\mu]^G

which has dimension |G \backslash (X_\lambda \times X_\mu)|. Writing \lambda = (\lambda_1, \ldots, \lambda_l) and \mu = (\mu_1, \ldots, \mu_{m}), let us pick (A_1, \ldots, A_l) \in X_\lambda and (B_1, \ldots, B_m)\in X_\mu. Then the orbit of the pair (g(X_\lambda), g(X_\mu)) satisfies:

|g(A_i) \cap g(B_j)|_{i, j} = |g(A_i \cap B_j)|_{i, j} \quad \text{ for } 1\le i \le l, 1 \le j \le m,

so the collection of these numbers is invariant over all g\in G.

Conversely, suppose (A_i), (B_j) and (A_i'), (B_j') are partitions of [d] satisfying:

|A_i| = |A_i'| = \lambda_i, \quad |B_j| = |B_j'| = \mu_j,\quad |A_i \cap B_j| = |A_i' \cap B_j'|

for all i, j. Then we can find g\in S_d mapping the pairwise intersection sets A_i \cap B_j to A_i' \cap B_j' so the pairs (A_i), (B_j) and (A_i'), (B_j') are in the same orbit. Hence the number of orbits is the number of solutions to

\sum_{i=1}^l a_{ij} = \mu_j, \qquad \sum_{j=1}^m a_{ij} = \lambda_i

in non-negative integers a_{ij}.

In particular, the above holds when we replace K by L so:

Conclusion. We have

\left< U_\mu, U_\lambda\right>_G = M_{\lambda\mu}.

blue-lin

Posted in Uncategorized | Tagged , , , | Leave a comment

Polynomials and Representations XVIII

Posted on May 24, 2016 by limsup

Littlewood-Richardson Coefficients

Recall that the Littlewood-Richardson coefficient satisfies:

c^\lambda_{\mu\nu} = \left<s_\lambda, s_\mu s_\nu\right> = \left< s_{\lambda/\mu}, s_\nu\right>.

By the previous article, for any SSYT U_1 of shape \nu, c^\lambda_{\mu\nu} is the number of skew SSYT of shape \lambda/\mu whose rectification is U_1. Since this number is independent of our choice of U_1 as long as its shape is \nu, we take the most natural one.

Definition. An SSYT is said to be canonical if its r-th row comprises of all r. For example, the following is a canonical SSYT of shape (5, 4, 3).

canonical_tableau

Note that an SSYT is canonical if and only if its shape is the same as its type. Thus c_{\mu\nu}^\lambda is the number of skew SSYT of shape \lambda/\mu such that its rectification is canonical of shape \nu.

blue-lin

Condition for Canonical SSYT

Definition. A word w = (w_1, w_2, \ldots, w_d) is a reverse lattice word if, for each i, the substring (w_i, w_{i+1}, \ldots, w_d) has at least as many 1’s as it has 2’s, at least as many 2’s as it has 3’s, etc.

A skew SSYT T is called a Littlewood-Richardson tableau if w(T) is a reverse lattice word.

For example, the following skew SSYT is a Littlewood-Richardson tableau since its word is (1,3,2,2,1,2,1,1).

littlewood_richardson_tableau

Lemma 1. An SSYT T is a Littlewood-Richardson tableau if and only if it is canonical.

Proof

Indeed, w(T) must end in 1, so the last entry of the first row is 1. Since each row is weakly increasing, the whole of first row is 1. Now the last entry of the second row is strictly greater than 1, but since w(T) is a reverse lattice word, that entry can only be 2. Thus the whole of second row comprises of 2’s. And so on. ♦

Lemma 2. If w and w' are Knuth-equivalent words, then w is a reverse lattice word if and only if w' is.

Proof

We may assume w' is obtained from w via R1 or R2. For convenience, we say that a word is OK if it has at least as many i as it has (i+1), for each i.

Consider R1; the other case is similar. We find a consecutive triplet (a,b,c) in w with c < a \le b, then replace (a,b,c) \mapsto (a, c, b) to form w'. Let us show that, for any word v, the four words on the left are OK if and only if the four words on the right are OK.

\displaystyle\left.\begin{aligned}a,b,c,& v\\b,c,& v\\c,& v\\ & v \end{aligned}\right\} \text{ OK } \iff \left.\begin{aligned} a,c,b,& v\\ c,b,& v\\ b,& v\\ & v \end{aligned}\right\} \text{ OK }

We only need to check the third word in each case. Suppose the LHS is OK.

  • If b,v is not OK, since v is OK there must be a d < b such that d and b occur an equal number of times in v.
  • Since b,c,v is OK, we must have d = c, and so any element between c and b (inclusive) occurs an equal number of times in v.
  • In particular, a, b, c each occurs an equal number of times in v.
  • Now if a < b, then b,c,v has more b‘s than a‘s, and if a = b, then a,b,c,v has more a‘s than c‘s, which contradicts the fact that the LHS is OK.

Now suppose the RHS is OK. If c,v is not OK, there is a d < c which occurs as many times in v as c. But now c,b,v is not OK, which gives a contradiction. ♦

For example, check that the rectification of the above Littlewood-Richardson tableau is:

littlewood_richardson_tableau_after_sliding

Exercise

Write out the proof for R2.

Now, putting the above two lemmas together, we have:

Corollary. A skew SSYT T is a Littlewood-Richardson tableau if and only if its rectification is canonical.

Proof

Indeed if T' is its rectification, then T is Littlewood-Richardson if and only if w(T) is a reverse lattice word; by lemma 2, this holds if and only if w(T') is a reverse lattice word. By lemma 1, this holds if and only if T' is canonical. ♦

We thus obtain:

Littlewood-Richardson Rule. c_{\mu\nu}^\lambda is the number of Littlewood-Richardson skew SSYT of shape \lambda/\mu and type \nu.

blue-lin

Example 1: Expanding Skew Schur Polynomials

Consider the skew Schur polynomial s_{\lambda/\mu} where \lambda = (4,3,2) and \mu = (2,1). To express s_{\lambda/\mu} as a linear sum of Schur polynomials, we only need to consider partitions \nu of |\lambda| - |\mu| = 6. Thus:

skew_schur_polynomial_example_2

We can also compute it directly by finding K_{\lambda/\mu, \nu} for various \nu, which gives:

\begin{aligned}s_{432/21} &= m_{42} + 2m_{411} + 2m_{33} + 6m_{321} + 11m_{3111} + 10m_{222} + 18m_{2211} + 33m_{21111} + 61m_{111111}.\end{aligned}

And the Schur polynomials give:

\begin{aligned} s_{42} &= m_{42} + m_{411} + m_{33} + 2m_{321} + 3m_{3111} + 3m_{222} + 4m_{2211} + 6m_{21111} + 9m_{111111},\\ s_{411} &= m_{411} + m_{321} + 3m_{3111} + m_{222} + 3m_{2211} + 6m_{21111} + 10m_{111111},\\ s_{33} &= m_{33} + m_{321} + m_{3111} + m_{222} + 2m_{2211} + 3m_{21111} + 5m_{111111}, \\ s_{321} &= m_{321} + 2m_{3111} + 2m_{222} + 4m_{2211} + 8m_{21111} + 16m_{111111}, \\ s_{222} &= m_{222} + m_{2211} + 2m_{21111} + 5m_{111111}. \end{aligned}

Example 2: Expanding Product of Schur Polynomials

Let us express s_{3}s_{21} as a linear sum of Schur polynomials. For each partition \lambda of 6, we have:

schur_polynomial_product_1

Swapping the two partitions (3) and (2,1) gives us an identical expansion, as expected.

schur_polynomial_product_2

Posted in Uncategorized | Tagged , , , , | Leave a comment

Polynomials and Representations XVII

Posted on May 22, 2016 by limsup

Two Important Results

In this article and the next, we will find a combinatorial way of computing the Littlewood-Richardson coefficient.

The key result we have so far is that given any word w there is a unique SSYT T (called the rectification of w) such that its word w(T) is Knuth-equivalent to w. This is related to the RSK construction as follows: recall that we obtain a 2-row array \small \begin{pmatrix} i_1 & \ldots i_d \\ j_1 & \ldots j_d\end{pmatrix}, then define a pair of SSYT of the same shape via:

  • P_0 = Q_0 = \emptyset,
  • P_{r+1} = P_r \leftarrow j_{r+1} and Q_{r+1} is obtained from Q_r by appending i_{r+1} so that it has the same shape as P_{r+1},
  • let (P, Q) = (P_d, Q_d).

In particular P = ((\emptyset \leftarrow j_1) \leftarrow j_2) \leftarrow \ldots and since w(T\leftarrow m) \equiv w(T) * (m) we get:

Observation. w(P) is Knuth-equivalent to the word (j_1, \ldots, j_d). In other words, P is the rectification of (j_1, \ldots, j_d).

blue-lin

First Theorem

Theorem 1. Suppose, in the RSK construction, the pair of SSYT (P, Q) of the same shape gives us the two-row matrix \small\begin{pmatrix} i_1 & \ldots & i_d \\ j_1 & \ldots & j_d \end{pmatrix}. Now let T be any SSYT and define the construction:

  • let P_0 = T and Q_0= \emptyset;
  • for each of r=0,\ldots,d-1, let P_{r+1} = P_{r} \leftarrow j_{r+1}, and Q_{r+1} be obtained from Q_r by attaching the new square of P_{i+1} to it, and filling in i_r.

The resulting Q_l is a skew SSYT whose rectification is Q.

Example

Suppose we have the matrix \small\begin{pmatrix} 1 & 1 & 1 & 2 & 2 \\ 1 & 2 & 2 & 1 & 3 \end{pmatrix} and the initial SSYT T = {\small \boxed{\begin{matrix} 1 & 2 \\ 2 \end{matrix}}}. This gives:

rsk_skew_tableau_version

The rectification of Q_5 is \small\boxed{\begin{matrix} 1 & 1 & 1 & 2 \\ 2\end{matrix}}, which is consistent with our claim.

Proof

Let w(T) = (t_1, t_2, \ldots, t_m). Add symbols s_1 < s_2 < \ldots < s_m which are strictly smaller than all i_r. (E.g. we can add a large constant to all existing labels). The RSK construction for 

\displaystyle \begin{pmatrix} s_1 & s_2 & \ldots & s_m \\ t_1 & t_2 & \ldots & t_m \end{pmatrix}

gives us a pair of SSYT. By the above observation, the first term of this pair is T; let the second term be U. Hence we get RSK correspondences:

rsk_skew_tableau_proofpic_new

The second correspondence is given in the conditions, while the third follows from

P_d = (T \leftarrow j_1) \leftarrow j_2 \leftarrow \ldots = ((\ldots ((\emptyset \leftarrow t_1) \leftarrow t_2) \leftarrow \ldots \leftarrow j_1) \leftarrow j_2) \ldots

and the definition of Q_d. By the symmetry theorem, swapping the two SSYT corresponds to swapping the two rows of the matrix and sorting the columns lexicographically so we get RSK correspondences:

rsk_skew_tableau_proofpic_2_new

Again by our observation above, the left matrix UQ_d satisfies

w(UQ_d) \equiv (s_1, \ldots, s_m) * some order of  (i_1, \ldots, i_d).

By the lemma here, dropping the m smallest terms still gives us Knuth-equivalent words. On the LHS, this gives the skew SSYT w(Q_d). On the RHS, this gives some order of (i_1, \ldots, i_d). From the first RSK correspondence, Q is the rectification of that same order of (i_1, \ldots, i_d). Hence w(Q_d) \equiv w(Q) and we are done. ♦

blue-lin

Second Theorem

Theorem 2. Let \lambda, \mu, \nu be partitions. Suppose T is an SSYT of shape \lambda and U is an SSYT of shape \nu. Then there is a bijection between:

  • pairs of SSYT (P, Q) of shapes \mu, \nu respectively, such that T = PQ;
  • skew SSYT U_1 of shape \lambda/\mu such that its rectification is U.

Recall that PQ is the rectification of the skew SSYT obtained by putting P below and Q above.

skew_tableau_and_double_tableaux_corr

Note

\lambda/\mu is well-defined only when \lambda_i \ge \mu_i for all i; otherwise, the second set is empty; it will follow from the proof that the first set is empty too.

Proof

Let (P,Q) be of shapes \mu,\nu respectively such that T=PQ. The RSK correspondence for (Q, U) gives us a two-row matrix:

\begin{pmatrix}i_1 & \ldots & i_d \\j_1 & \ldots & j_d\end{pmatrix}.

Let T_1 be the SSYT obtained from P by inserting j_1, \ldots, j_d and U_1 be the skew SSYT obtained by putting i_1, \ldots, i_d in the new empty boxes. By construction we have T_1 = PQ = T, so U_1 has shape \text{shape}(T) / \text{shape}(P) = \lambda/\mu. By theorem 1, the rectification of U_1 is U.

Conversely, suppose we are given skew U_1 of shape \lambda/\mu such that U_1 \equiv U. Let T_1 be the SSYT obtained from U_1 by attaching an SSYT V of shape \mu and entries smaller than those of U_1.

double_tableaux_proof

Then (T, T_1) corresponds via RSK to a two-row matrix:

\begin{pmatrix}x_1 & \ldots & x_m & i_1 & \ldots & i_d \\y_1 & \ldots & y_m & j_1 & \ldots & j_d\end{pmatrix}

where x_1, \ldots, x_m are from V and i_1, \ldots, i_d are from U_1. By RSK, the first m columns correspond to a pair of SSYT (P, V) of shape \mu. The remaining d columns correspond to a pair (Q, U) since U is the rectification of U_1. Hence Q has shape \nu. Finally we have T = P \leftarrow j_1 \leftarrow j_2 \leftarrow \ldots which gives T=PQ as desired. ♦

blue-lin

Our main interest is in the following.

Corollary. For each SSYT U of shape \nu, the number of skew SSYT U_1 of shape \lambda/\mu such that U_1 \equiv U is dependent only on \mu, \nu, \lambda, and independent of the choice of U.

Denote this number by d^\lambda_{\mu\nu}. Recall that the skew Schur function

\displaystyle s_{\lambda/\mu} = \sum_T x^T over all skew SSYT T of shape \lambda/\mu.

Let T' be the rectification of T. By the corollary, if T' has shape \nu, there are exactly d^\lambda_{\mu\nu} possibilities for T. Hence,

\displaystyle s_{\lambda/\mu} = \sum_\nu d^\lambda_{\mu\nu}\sum_{T'} x^{T'}, over all partitions \nu and SSYT T' of shape \nu.

\displaystyle \implies s_{\lambda/\mu} = \sum_\nu d^{\lambda}_{\mu\nu} s_\nu.

So \displaystyle c_{\mu\nu}^\lambda = \left< s_{\lambda/\mu}, s_\nu\right> = d_{\mu\nu}^\lambda and our d_{\mu\nu}^\lambda is precisely the Littlewood-Richardson coefficient, and we get a combinatorial interpretation:

Summary. For any SSYT U_1 of shape \nu, c_{\mu\nu}^\lambda is the number of skew SSYT of shape \lambda/\mu whose rectification is U_1.

blue-lin

Posted in Uncategorized | Tagged , , , , | Leave a comment

Polynomials and Representations XVI

Posted on May 20, 2016 by limsup

Here is the main problem we are trying to solve today.

Word Problem

Given a word w = (w_1, w_2, \ldots, w_m), let us consider k disjoint subwords of w which are weakly increasing. For example if w = (1, 1, 5, 4, 2, 5, 4, 6, 7), then we can pick two or three disjoint subwords as follows:

subwords_examples

For each k\ge 1, we wish to compute L(w, k), the maximum length sums of disjoint weakly increasing subwords. In our example, L(w, 3) = 9. However, L(w, 2) \ge 8 since we can add the second ‘5’ to the circles, thus using up 8 numbers in the word. It turns out we do have L(w,2) = 8 although this is not obvious at the moment.

There is at least one case where computing L(w, k) is trivial.

Proposition 1. If w = w(T) for some SSYT T of shape \lambda, then for each k we have:

L(w, k) = \lambda_1 + \lambda_2 + \ldots + \lambda_k.

Proof

Indeed if T has rows w_1, w_2, \ldots, w_l, then w(T) = w_l * w_{l-1} * \ldots * w_1 and the words w_1, \ldots, w_k are disjoint weakly increasing words of the required length sum. Hence L(w, k) \ge \lambda_1 + \ldots + \lambda_k.

Conversely, if w_1', \ldots, w_k' are disjoint weakly increasing subwords of w(T), the numbers in each w_i' are from different columns of T. So in each column of T, at most k entries are used among the w_i' and the length sum of w_1', \ldots, w_k' is at most \lambda_1 + \ldots + \lambda_k. ♦

blue-lin

General Solution

The good news is, every case can be reduced to the SSYT case. Indeed, given any word w, we can write w = w(T) for some skew SSYT T. Now we perform sliding operations to turn T into an SSYT T'. By the next result, L(w, k) = L(w(T), k) = L(w(T'), k) for all k, so we can revert to the above special case.

Proposition 2. If w, w' are Knuth-equivalent words, then L(w, k) = L(w', k).

Proof

We may assume w' is obtained from w by rule R1 or R2. Let us consider each case.

R1: in w we have a consecutive triplet (a, b, c) with c < a \le b; we swap b and c to get w'. In most instances, disjoint weakly increasing subwords of w will remain so in w' and vice versa. The only problem is when a subword of w' contains c,b, say w_1 = \ldots, c, b,\ldots. If no subword contains a, we can replace c,b with a,b and the resulting word is still weakly increasing. If not, we swap the heads:

\displaystyle\left.\begin{aligned}w_1 = \text{(seq 1)}, &c, b, \ldots\\ w_2 = \text{(seq 2)}, &a, \ldots \end{aligned}\right\} \text{subwords of } w' \implies\left.\begin{aligned}w_1 = \text{(seq 2)}, &a, b, \ldots\\w_2 = \text{(seq 1)}, &c, \ldots \end{aligned}\right\} \text{subwords of } w

which are still weakly increasing.

R2: similarly, in w we have a consecutive triplet (a, b, c) with a\le c <b; swap a and b to get w'. The critical case is now as follows:

\displaystyle\left.\begin{aligned} w_1 = \ldots, a, b, &\text{(seq 1)}\\w_2 = \ldots, c, &\text{(seq 2)} \end{aligned}\right\} \text{subwords of } w \implies \left. \begin{aligned} w_1 = \ldots, a, c, &\text{(seq 2)}\\w_2 = \ldots, b, &\text{(seq 1)}\end{aligned}\right\} \text{subwords of } w'

This completes the proof. ♦

Summary

Thus we have:

Algorithm. To compute L(w, k), write w = w(T) for a skew SSYT T, perform the sliding algorithm to turn T into an SSYT T' of shape \lambda. Now we have:

L(w, k) = \lambda_1 + \lambda_2 + \ldots + \lambda_k for all k\ge 1.

E.g. in our initial example of (1, 1, 5, 4, 2, 5, 4, 6, 7), first write it as a word of some skew SSYT, then perform sliding to turn it into an SSYT.

word_problem_solution

It follows that L(w, 1) = 6, L(w, 2) = 8 and L(w, 3) = 9.

Question to Ponder

Besides computing L(w, k), what is an efficient way to compute explicit disjoint subwords with the desired length sum?

blue-lin

Uniqueness of SSYT for Word

We need the following lemma for our theorem later.

Lemma. If w \equiv w' and w_0 (resp. w_0') is obtained from w (resp. w') by removing the largest element, then w_0 \equiv w_0'. The same holds for the smallest element.

Here, if the maximal element k of w occurs more than once, the rightmost occurrence is taken to be the largest. Similarly, the leftmost occurrence of the minimal element is the smallest.

Proof

We may assume w' is obtained from w by R1 or R2, i.e. by replacing a consecutive triplet:

\displaystyle (a, b, c) \mapsto \begin{cases}(a, c, b), \quad &\text{ if } c < a \le b, \\(b, a, c), \quad &\text{ if } a \le c < b. \end{cases}

If none of a,b,c is maximal, we are done. Otherwise, in both cases, b is maximal; after removing it, we get (a,c) in w_0 and w_0'.

In the case the smallest element is removed, in the first case we remove c and obtain (a,b) in both w_0 and w_0'. In the second case, we remove a and obtain (b,c) in both w_0 and w_0'. ♦

Now we have enough tools to prove the following result we claimed earlier.

Theorem. For any word w, there is a unique SSYT T such that w \equiv w(T).

We call this T the rectification of the word w. For a skew SSYT T', the rectification of w(T') is also called the rectification of T'.

Proof

Existence of T was proven earlier; we now prove uniqueness, i.e. for any SSYT T, T',

w(T) \equiv w(T') \implies T = T'.

By proposition 2, the shape \lambda of T satisfies

\lambda_1 +\lambda_2 + \ldots + \lambda_k = L(w(T),k) = L(w(T'), k)

so T and T' have the same shape. Now we proceed by induction on |\lambda|; when |\lambda| \le 1 we clearly have T = T'.

Suppose |\lambda| \ge 2 and m is the largest element in w(T) and w(T'); if this occurs more than once, we take the rightmost occurrence. Note that m must lie in a corner square of T and T'. Removing it thus gives us SSYT T_0 and T_0'. By the above lemma, we have

w(T) \equiv w(T') \implies w(T_0) \equiv w(T_0').

Since T_0 has one less square than T, by induction hypothesis T_0 = T_0'. And since T and T' have the same shape, we have T = T'. ♦

blue-lin

Summary

There is a bijection:

summary_equivalence_words_and_ssyt

The bijection is preserved when we drop the maximum or minimum element in either case. Clearly concatenation preserves Knuth-equivalence:

w_1 \equiv w_1',\ w_2 \equiv w_2' \implies w_1 * w_2 \equiv w_1' * w_2'

since any sequence of R1’s and R2’s performed on w_1 \mapsto w_1' can be done on w_1 * w_2 \mapsto w_1' * w_2. Thus this gives an associative product operation on the set of SSYT: given T, T', let T*T' be the rectification of w(T) * w(T'). This motivates the product operation we defined earlier.

Posted in Uncategorized | Tagged , , , , | Leave a comment

Polynomials and Representations XV

Posted on May 18, 2016 by limsup

Tableaux and Words

In our context, a word is a sequence of positive integers; concatenation of words is denoted by w * w'. Given a skew SSYT T, the corresponding word w(T) is obtained by taking the tableau entries from left to right, then bottom to top. For example the following skew SSYT gives w(T) = (1, 4, 2, 4, 5, 2, 3, 4, 5, 1, 1, 4, 6).

ssyt_to_word_example

The following are quite easy to verify.

  • If T is an SSYT, then it can be recovered from w(T).
    • We pick the longest weakly increasing sequence starting from the first number; this forms the last row. Repeat with the next number to obtain the second-to-last row, etc. E.g. given (4, 5, 3, 3, 4, 6, 1, 2, 3, 3, 5, 7), we get a three-row SSYT comprising of (1, 2, 3, 3, 5, 7), (3, 3, 4, 6) and (4, 5).
  • Not every word occurs as w(T) from some SSYT T.
    • E.g. (1, 2, 1, 2) does not come from an SSYT.
  • However, every word occurs as w(T) for some skew SSYT. E.g. just place the n elements of the sequence diagonally: 1st row and n-th square, 2nd row and (n-1)-th square etc.
  • In general, a skew SSYT T cannot be uniquely recovered from w(T).
    • E.g. for (1, 2), we can either take the SSYT (1, 2), or the skew diagram (2,1)/(1) and fill in 1, 2.

blue-lin

Words and Row Insertion

Next we formulate rules such that row-inserting (bumping) an entry m into an SSYT T is equivalent to concatenation:

w(T \leftarrow m) \equiv w(T) * (m).

Suppose we have a row (v_1, \ldots, v_n) in the SSYT with m added to the end, and assume

v_1 \le v_2 \le \ldots \le v_{i-1} \le m < v_{i} \le \ldots \le v_n,

so that m bumps off v_{i} and we get (v_1, \ldots, v_n, m) \mapsto (v_i, v_1,\ldots, v_{i-1}, m, v_{i+1}, \ldots, v_n). Break this down into a series of steps:

\begin{aligned} (v_1, \ldots, \boxed{v_{n-1}, v_n, m}) &\mapsto (v_1, \ldots, v_{n-1}, m, v_n) \\&\ldots \\&\mapsto (v_1, \ldots, v_{i-1}, v_i, m, \ldots, v_n).\end{aligned}

From this we obtain the first rule:

Rule R1. For any consecutive (a,b,c) in the word satisfying c <a \le b, we switch (a,b,c) \mapsto (a,c,b).

Next, to shift v_i to the beginning of the row, we break it down as follows:

\begin{aligned}(v_1, \ldots, \boxed{v_{i-1}, v_i, m}, \ldots, v_n) &\mapsto(v_1, \ldots, v_{i}, v_{i-1}, m, \ldots, v_n) \\ &\ldots\\ &\mapsto (v_i, v_1, \ldots, v_{i-1}, m, \ldots, v_n).\end{aligned}

From here, we obtain the second rule:

Rule R2. For any consecutive (a,b,c) in the word satisfying a \le c <b, we switch (a,b,c) \mapsto (b,a,c).

Example

Suppose we insert (1, 2, 2, 3, 4, 5, 5) \leftarrow 3. Applying R1 and R2 gives:

\begin{aligned} &(1, 2, 3, 4, \overset{R1}{\boxed{5, 5, 3}}) \mapsto (1, 2, 3, \overset{R1}{\boxed{4, 5, 3}}, 5)\mapsto (1, 2, \overset{R2}{\boxed{3, 4, 3}}, 5, 5)\\ \mapsto &(1, \overset{R2}{\boxed{2, 4, 3}}, 3, 5, 5) \mapsto (\overset{R2}{\boxed{1, 4, 2}}, 3, 3, 5, 5)\mapsto (4, 1, 2, 3, 3, 5, 5).\\ \end{aligned}

Now we wish to revert the inserting process, so we will consider reverse of R1 and R2 as well, denoted by R1′ and R2′ respectively.

Summary of Rules

Given a consecutive triplet (a,b,c) in the word, we consider the following distinct cases:

  • a \le b \le c or a > b > c: no change;
  • c < a \le b: switch to (a, c, b) by R1;
  • a \le c < b: switch to (b, a, c) by R2;
  • b < a \le c: switch to (a, c, b) by R1′;
  • b \le c < a: switch to (b, a, c) by R2′.

One checks that these cases are disjoint and cover all possibilities. Two words are said to be Knuth-equivalent, written as w\equiv w', if we can obtain one from the other via the above 4 operations.

Mnemonic

The following diagram helps us in recalling R1 and R2.

\begin{aligned} c < a\le b\ : \quad &\left(\ \boxed{\begin{matrix}a & b\end{matrix}}\ \leftarrow\ c\ \right)\ = \boxed{\begin{matrix} c & b \\ a\end{matrix}} \\ a\le c < b\ :\quad &\left(\ \boxed{\begin{matrix}a & b\end{matrix}}\ \leftarrow\ c\ \right)\ = \boxed{\begin{matrix} a & c \\ b\end{matrix}} \end{aligned}.

blue-lin

Consequences of Equivalence

From our construction of R1 and R2, we immediately have:

Proposition 1. w(T \leftarrow m) \equiv w(T) * (m).

The following result is less trivial.

Proposition 2. If T' is obtained by sliding an inner corner of skew SSYT T, then w(T') \equiv w(T).

Proof

Clearly, horizontal sliding does not change the word, so we will only consider vertical sliding. By trimming off excess elements in the two rows:

two_row_vertical_slide

we may assume the two rows have the same length. We will prove that the corresponding words are Knuth-equivalent via induction on p. Write \vec n for (n_1, \ldots, n_q), \vec m for (m_1, \ldots, m_p) etc. First consider the case p=0, i.e. we need to show x \vec n \vec v \equiv \vec n x \vec v.

  • Imagine performing row insertion for v_1 into x \vec n. Since x \le v_1 <n_1, this bumps out n_1 and we transform x\vec n v_1 to n_1 x v_1 n_2 n_3 \ldots.
  • Inserting v_2 into this row then bumps out n_2, and we obtain n_1 n_2 x v_1 v_2 n_3 \ldots. Moving on, we eventually obtain \vec n x \vec v as desired.

Now assume p>0. Write \vec u' = (u_2, \ldots, u_p) and  \vec m' = (m_2, \ldots, m_p) so that \vec u = (u_1) * \vec u' and \vec m = (m_1) * \vec m'. We need to show

m_1 \vec m' \boxed{x \vec n u_1 \vec u'} \vec v\ \overset{?}\equiv\ m_1 \vec m' \boxed{\vec n u_1 \vec u' x} \vec v.

Inserting u_1 into the row m_1 \vec m' x \vec n bumps off m_1 which gives m_1 u_1 \vec m' x \vec n. Thus the LHS is equivalent to m_1 u_1 \vec m' x \vec n \vec u' \vec v. By induction hypothesis for p-1, this is equivalent to m_1 u_1 \vec m' \vec n \vec u' x \vec v.

On the other hand, on the RHS above we insert u_1 into the row m_1 \vec m' \vec n to give m_1 u_1 \vec m' \vec n. Hence the RHS is equivalent to m_1 u_1 \vec m' \vec n \vec u' x \vec v. This completes the proof. ♦

Corollary. Every word w is Knuth-equivalent to w(T) for some SSYT T.

Proof

Indeed write w = w(T') for some skew SSYT T'. Apply the sliding algorithm to it to obtain an SSYT T. By proposition 2, w(T') \equiv w(T). ♦

This T will later turn out to be unique. 🙂

blue-lin

Additional Result

Finally, the following result is interesting but will not be used.

Lemma. If the skew tableau T is cut into T' and T'' by a horizontal or vertical line (where T' is respectively left or above), then w(T) \equiv w(T') * w(T'').

Proof

In the case of horizontal cut, we in fact have w(T) = w(T') * w(T'') so the result is trivial. Now suppose we have a vertical cut as follows.

skew_tableau_split_vertically

Start removing the inner corners from T', starting from the rightmost column. E.g. in the above diagram, we remove the corner labelled a, then the one above etc. Note that upon removing a, the column beneath it gets shifted up one unit. Eventually, we obtain the LHS diagram. By proposition 2, the above two tableaux have equivalent words and the tableau T_1 on the right gives w(T_1) = w(T') * w(T''). ♦

blue-lin

Posted in Uncategorized | Tagged , , , , | Leave a comment

Polynomials and Representations XIV

Posted on May 16, 2016 by limsup

In this article, we describe a way of removing the internal squares of a skew SSYT to turn it into an SSYT.

Definition. First write the skew diagram as \lambda/\mu; we define an inside corner to be a square in \mu such that there is no square to its right or below lying within \mu.

Note that there is some ambiguity in this definition, since there is generally more than one way of writing a skew diagram in the form \lambda/\mu. For example if \lambda = (3, 2, 1) and \mu = (2,2), then \lambda/\mu = \lambda'/\mu' where \lambda' = (3,1,1) and \mu' = (2,1).

equal_skew_tableaux

In the left diagram, there is only one inside square at (2, 2) while in the right diagram there are two inside squares at (1, 2) and (2, 1).  Henceforth, our construction is performed with respect to a fixed representation of the skew diagram as \lambda/\mu.

blue-lin

Removing an Inside Corner

Now we describe the procedure. Let T be a skew SSYT; pick any inside corner S of T, a blank square. At each step, we look at its right and below.

  • If there are numbers to its right and below, we swap S with the smaller value; if both numbers are equal, the one below is taken to be smaller.
  • If there is only one number to its right or below, we swap S with that.
  • If there are no numbers to its right and below, we can just remove S.

Note that at each step, the rows are guaranteed to be weakly increasing and the columns strictly increasing, so at the end we get another skew tableaux but with one less empty square.

Example

skew_tableaux_sliding

Lemma. The process is reversible, i.e. starting from the skew tableaux at the end, and an additional square at the end of a row such that the union is still a skew diagram, we can reverse the process of sliding.

Proof

One observes that at each step of the sliding process, the move applied is the only possible one such that the rows remains weakly increasing and columns strictly increasing, i.e. the move is the only legal one available.

The same holds for the reverse sliding process: at each step, we take the empty square and look at its left and above, then swap with the larger one; if both are equal, we swap with the one above. ♦

blue-lin

Sliding Algorithm

Definition. The sliding algorithm on a skew SSYT T is as follows: we iteratively remove inner squares as above until we get an SSYT T'.

It is a non-trivial result that the resulting T' is independent of our order of removal, or our choice of expression \lambda / \mu.

Exercise

There are two ways to perform the sliding algorithm on the following skew SSYT. Check that they both lead to the same SSYT.

skew_ssyt_exercise

Assuming the above uniqueness result, we define the following.

Definition. Given two SSYT T and T', their product T*T' is obtained by placing T below and T' on the right to form a skew SSYT as follows:

tableaux_product_skew

then performing the sliding algorithm to turn it into an SSYT.

It is also true that the product is associative. All these will be proven within the next few articles.

blue-lin

Posted in Uncategorized | Tagged , , , | Leave a comment