Commutative Algebra 5

Posted on March 23, 2020 by limsup

Morphisms in Algebraic Geometry

Next we study the “nice” functions between closed subspaces of \mathbb A^n.

Definition.

Suppose V\subseteq \mathbb A^n and W\subseteq A^m are closed subsets. A morphism f:V\to W is a function which can be expressed as:

f(v_1, \ldots, v_n) = (f_1(v_1, \ldots, v_n), f_2(v_1, \ldots, v_n), \ldots, f_m(v_1, \ldots, v_n))

for some polynomials f_1, f_2, \ldots, f_m \in k[X_1, \ldots, X_n]. We also say f is a regular map.

Example

  1. Let V \subseteq \mathbb A^n be any closed subset. Regular maps of the form V \to \mathbb A^1 are given by polynomials f \in k[X_1, \ldots, X_n].
  2. Take V = \mathbb A^1 and W = \{(x, y, z) \in \mathbb A^3 : x^2 + y^2 = z^2\}. Define f:V\to W by t \mapsto (t^2 - 1, 2t, t^2 + 1). We write this as x = t^2 - 1, y = 2t, z = t^2 + 1.
  3. Take V = \mathbb A^1 and W = \{(x, y) \in \mathbb A^2 : y^2 = x^3\}. Define f:V\to W by t\mapsto (t^2, t^3). We write this as x = t^2, y = t^3.

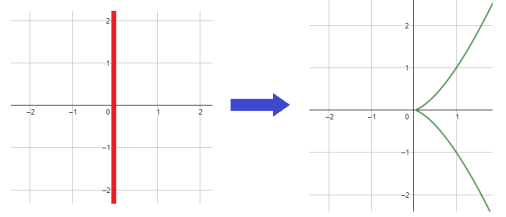
morphism_of_curves

[Example 3: image edited from GeoGebra plot.]

The first example, although basic, is of huge importance.

Definition.

A regular function for a closed subset V\subseteq \mathbb A^n is a morphism of the form V\to \mathbb A^1.

The set of such functions is called the coordinate ring of V and is denoted by k[V].

Note

Each regular function is given by f\in k[X_1, \ldots, X_n] and two polynomials f, g induce the same function on V if and only if

(\forall P \in V, f(P) = g(P)) \iff (\forall P \in V, (f-g)(P) = 0) \iff f-g \in I(V).

Thus we have k[V] \cong k[X_1, \ldots, X_n]/I(V), which gives k[V] its ring structure. To describe this ring structure in terms of regular functions, we have:

\text{morphisms } f, g : V \to \mathbb A^1 \implies \begin{cases} (f+g) : V\to \mathbb A^1, \ &P \mapsto f(P) + g(P) \in k, \\ (f\cdot g) : V\to \mathbb A^1, \ &P \mapsto f(P)g(P)\in k. \end{cases}

blue-lin

Morphisms in Algebra

General morphisms f:V\to W can now be described in the language of their coordinate rings.

Proposition 1.

Let V\subseteq \mathbb A^n and W\subseteq \mathbb A^m be closed. There is a bijection between:

  • morphisms f:V\to W;
  • ring homomorphisms f^* : k[W] \to k[V] which are linear over k.

Note

The second condition can be rephrased as: k[W] \to k[V] is a homomorphism of k-algebras. In a later article, we will cover algebras over a ring in greater detail.

Proof

Given a morphism f:V\to W, upon composing with a regular function g : W\to \mathbb A^1, we obtain a regular function g\circ f : V\to \mathbb A^1 of V. This gives a ring homomorphism k[W] \to k[V] which is clearly linear over k.

Conversely, suppose \phi : k[W] \to k[V] is a ring homomorphism which is linear over k. Let \overline X_1, \ldots, \overline X_m be the images of  X_1, \ldots, X_m in k[W] = k[X_1, \ldots, X_m]/I(W). Let f_i = \phi(\overline X_i) \in k[V] which is a regular function V\to \mathbb A^1. We claim that the function

f : V \to \mathbb A^m, \quad f(P) := (f_1(P), \ldots, f_m(P))

has image in W. Indeed for any g\in I(W)\subseteq k[X_1, \ldots, X_m] we have

g\circ f = g(f_1, \ldots, f_m) = g(\phi(\overline X_1), \ldots, \phi(\overline X_m)) = \phi(g(\overline X_1, \ldots, \overline X_m)) = \phi(\overline{g(X_1, \ldots, X_m)})

which is 0 since \overline g =0 in k[W]. This creates a bijection. ♦

Note

In order to swap g(\phi(\ldots)) = \phi(g(\ldots)) we require \phi to be a ring homomorphism linear over k. E.g. if g = \alpha X_1^2 +\beta X_2 with \alpha, \beta\in k then

g(\phi(\overline X_1), \phi(\overline X_2)) = \alpha\phi(\overline X_1)^2 + \beta \phi(\overline X_2) = \phi(\alpha \overline X_1^2 + \beta \overline X_2) = \phi(g(\overline X_1, \overline X_2)).

The following properties are obvious:

Lemma.

  • For any closed set V, we have (1_V)^* = 1_{k[V]}.
  • For any morphisms f:V \to V', g:V' \to V'' of closed sets we have

(g\circ f)^* =f^* \circ g^* : k[V''] \longrightarrow k[V].

Proof

The first is clear. For the second, pick any h\in k[V''], a regular map V''\to \mathbb A^1. Then

f^*(g^*(h)) = f^*(h\circ g) = (h \circ g)\circ f = h\circ (g\circ f) = (g\circ f)^*(h). ♦

Examples

Let us interpret the earlier examples as homomorphisms k[W] \to k[V].

Example 2. We have:

f : \mathbb A^1 \to \{(x, y, z) \in \mathbb A^3 : x^2 + y^2 = z^2\}, \quad t \mapsto (t^2 - 1, 2t, t^2 + 1).

We wrote this as x = t^2 - 1, y = 2t, z = t^2 + 1 for a reason, for f corresponds to:

f^* : k[X, Y, Z]/(X^2 + Y^2 - Z^2) \longrightarrow k[T], \quad X \mapsto T^2 - 1, Y \mapsto 2T, Z \mapsto T^2 + 1.

Example 3. Similarly

f : \mathbb A^1 \to \{(x,y) \in \mathbb A^2 : y^2 = x^3\}, \quad t\mapsto (t^2, t^3)

was written as x = t^2, y = t^3. Algebraically,

f^* : k[X,Y]/(Y^2 - X^3) \longrightarrow k[T], \quad X \mapsto T^2, Y \mapsto T^3.

blue-lin

Properties

Since we defined a topology on closed sets, the morphisms should be continuous.

Proposition 2.

A morphism f : (V\subseteq \mathbb A^n) \to (W\subseteq \mathbb A^m) is a continuous map, with respect to the subspace topology on both sets.

Proof

Let W’ be a closed subset of W, so it is also a closed subset of \mathbb A^m. We need to show f^{-1}(W') is closed in V (equivalently, in \mathbb A^n). Now W’ can be written as

W' = \{Q \in W: \text{ for each } g \in S', g(Q) = 0\}

for some subset S' \subseteq k[X_1, \ldots, X_m]. It follows that

f^{-1}(W') = \{P \in V : \text{ for each } g \in S', g(f(P)) = 0\}

is cut out from V by equations \{g\circ f : g\in S'\}. Hence f^{-1}(W') is closed. ♦

Isomorphisms

Definition.

Closed subsets V \subseteq \mathbb A^n and W\subseteq \mathbb A^m are said to be isomorphic if there exist regular maps f : V\to W and g:W\to V such that g\circ f = 1_V and f\circ g = 1_W.

This implies:

f^* : k[W] \to k[V],\ g^* : k[V] \to k[W], \quad f^*\circ g^* = 1_{k[V]}, \ g^* \circ f^* = 1_{k[W]}.

Hence isomorphism of the closed subsets corresponds to isomorphism of the underlying k-algebras!

Example

Let us take example 3 from above, where f : \mathbb A^1 \to \{(x,y) \in \mathbb A^2 : y^2 = x^3\} is defined by f(t) = (t^2, t^3). Note that f is bijective on the points, and it corresponds to:

f^* : k[X,Y]/(Y^2 - X^3) \longrightarrow k[T], \quad X \mapsto T^2, Y \mapsto T^3.

The image of f^* is not surjective since it does not contain T. We have thus learnt:

warningThere exist bijective regular maps V\to W which are not isomorphisms.

blue-lin

More General Correspondence

Putting it together, we obtain the following bijective correspondences:

algebraic_geometry_corr_v2

  • The top correspondence was the original one.
  • The left correspondence follows from point-set topology.
  • The right correspondence follows from the correspondence between ideals of A/\mathfrak a and ideals of A containing \mathfrak a.
    • The correspondence preserves radical ideals because \mathfrak b is a radical ideal of A if and only if A/\mathfrak b is a reduced ring; now apply (A/\mathfrak a)\, /\, (\mathfrak b/\mathfrak a) \cong A/\mathfrak a.

Summary.

In other words, we have a bijection between radical ideals of the coordinate ring k[V] and closed subsets of V. This enables us to look at V and its coordinate ring k[V], ignoring the ambient affine space it sits in.

blue-lin

This entry was posted in Advanced Algebra and tagged , , , , , . Bookmark the permalink.

2 Responses to Commutative Algebra 5

  1. Vanya says:
    April 5, 2020 at 5:48 am

    Could you please explain further the last sentence “This enables us to look at V and its coordinate ring k[V], ignoring the ambient affine space it sits in.”? Is it not the case that we need to consider some ambient affine space while we consider some closed subspace V it sits in?

    Reply

Leave a Reply

Fill in your details below or click an icon to log in:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s