Topology: Complete Metric Spaces

[ This article was updated on 8 Mar 13; the universal property is now in terms of Cauchy-continuous maps. ]

On an intuitive level, a complete metric space is one where there are “no gaps”. Formally, we have:

Definition. A metric space (X, d) is said to be complete if every Cauchy sequence in X converges.

Completeness is not a topological property, i.e. one can’t infer whether a metric space is complete just by looking at the underlying topological space. For example, (0, 1) and R are homeomorphic as topological spaces, but the former is not complete (since the sequence (1/n) is Cauchy but doesn’t converge) and the latter is. Clearly, not every subspace of a complete metric space is complete. E.g. R – {0} is not complete since the sequence (1/n) doesn’t converge. However, we have:

Proposition 1. A subset of a complete metric space X is complete if and only if it’s closed in X.

Proof.

Both directions use theorem 1 here. If Y is closed in X, then any Cauchy sequence in Y is also Cauchy in X and hence must converge to some a in X; then a must lie in Y by the theorem.

Conversely, if Y is a non-closed subset of X, then there is a sequence in Y converging to a in X, outside Y. This sequence is Cauchy since it’s convergent in X, but it doesn’t converge in Y; thus Y is not complete. ♦

Proposition 2. If $(X, d_X)$ and $(Y, d_Y)$ are complete metric spaces, then so is $(X\times Y, d)$ where d can be any one of the following metrics:

$((x,y), (x',y')) \mapsto \sqrt{d_X(x,x')^2 + d_Y(y,y')^2}$ ;

$((x,y), (x',y')) \mapsto d_X(x,x') + d_Y(y,y')$ ;

$((x,y), (x',y')) \mapsto \max(d_X(x,x'), d_Y(y,y'))$ .

Proof.

We know (from proposition 3 here) that if a sequence $(x_n, y_n)$ in X × Y is Cauchy, then $(x_n), (y_n)$ are Cauchy in X and Y respectively. Hence, they’re both convergent, say, to $a\in X, b\in Y.$ Thus, $(x_n, y_n) \to (a, b)$ is convergent. ♦

Exercise

Suppose $X_1, X_2, \ldots$ is a countably infinite collection of complete metric spaces. Construct a metric on $X:=\prod_{n=1}^\infty X_n$ as before. Is the resulting metric space complete?

Answer (highlight to read) :

Yes, each projection map π_n : X → X_n is uniformly continuous. So a Cauchy sequence (x_n)₁, (x_n)₂, (x_n)₃, … gives rise to a Cauchy sequence in each X_n. Each of these converges, to say, a_n in X_n. Then by proposition 4 here, we see that (x_n)₁, (x_n)₂, (x_n)₃, … converges to (a_n). ♦

Completion of Metric Space

It turns out there’s a unique way of embedding any metric space into a “smallest” complete metric space.

Definition. A metric space Y is a completion of metric space X if:

X is a metric subspace of Y;

Y is complete; and

X is dense in Y.

Suppose $X\subseteq Y$ satisfies the first two conditions. Then we take $X\subseteq Z:=\text{cl}_Y(X)\subseteq Y.$ Now Z is closed in Y so it is complete by proposition 1 above. Furthermore, X is dense in Z by definition. So $X\subseteq Z$ is now a completion. In other words, the third condition enforces a minimality condition on Y. One can visualise Y as filling up the gaps of X.

Classical example: the completion of Q, under the Euclidean metric, is R.

The key property of the completion is the following.

Universal Property of Completion. Suppose $X\subseteq Y$ is a completion. Then:

for any Cauchy-continuous map $f:X \to Z$ to a complete metric space Z, there is a unique continuous $g:Y\to Z$ such that $g|_X = f.$

Minor Note.

Since g is continuous, it’s automatically Cauchy-continuous here since Y is complete: indeed, if $(y_n)$ is a Cauchy sequence in Y, then it converges to some y, so $(f(y_n))\to f(y)$ is convergent and must also be Cauchy.

Proof.

Uniqueness: if g, g’ satisfy $g|_X = g'|_X$ then since X is dense in Y and Z is Hausdorff, we have g = g’.

Only existence remains: we denote the metric of X and Y by d and that of Z by d’.

Suppose $y\in Y;$ since X is dense in Y, y is a limit of a sequence (x_n) in X. Then (x_n) is Cauchy and since f is Cauchy-continuous, (f(x_n)) is Cauchy in Z. So (f(x_n)) converges to some z and we let g(y) = z.

To show g is well-defined: suppose $(x_n), (x_n') \to y.$ We need to show $(f(x_n)), (f(x_n'))$ have the same limit. It suffices to show $d'(f(x_n), f(x_n')) \to 0$ as n → ∞.

For each ε>0, pick δ>0 such that whenever d(x, y) < δ, we have d’(f(x), f(y)) < ε.
Given this δ, pick N such that when n>N, we have $d(x_n, y)<\frac\delta 2$ and $d(x_n', y)<\frac\delta 2.$
Then when n>N, $d(x_n, x_n') \le d(x_n, y)+d(y, x_n') < \delta \implies d(f(x_n), f(x_n')) < \epsilon.$

Clearly $g|_X = f$ since if $y\in X$ we can pick the constant sequence (y, y, …) in X.

Finally, we need to show g is continuous. By theorem 6 here, it suffices to show that if $(y_n)\to y,$ then $(g(y_n))\to g(y).$ Now since X is dense in Y, we can pick a sequence $(x_n)$ such that $d(x_n, y_n)<\frac 1 n.$ This gives $(x_n)\to y$ also. From our definition of g, we must have $(g(x_n)) = (f(x_n)) \to g(y)$ so we’re done. ♦

Exercise

Prove that if f had been uniformly continuous, so is the induced g.

Answer (highlight to read).

The following replaces the last paragraph in the proof of universal property.

Let ε>0. There exists δ>0 such that whenever x, x’ in X satisfies d(x, x’) < δ, we have d’(f(x), f(x’)) < ε/2. Now suppose y, y’ in Y satisfy d(y, y’) < δ/2.

Pick sequences (x_n), (x_n‘) in X such that (x_n) → y and (x_n‘) → y’.
For large enough n, d(x_n, y) < δ/4 and d(x_n‘, y’) < δ/4 so we get d(x_n, x_n‘) ≤ d(x_n, y) + d(y, y’) + d(y’, x_n‘) < δ.
Thus, for n big, d’(f(x_n), f(x_n‘)) < ε/2.
Since f(x_n) → g(y) and f(x_n‘) → g(y’) by definition, we can pick a large n such that d’(f(x_n), g(y)) < ε/4 and d’(f(x_n‘), g(y’)) < ε/4.
This gives d’(g(y), g(y’)) ≤ d’(g(y), f(x_n)) + d(f(x_n), f(x_n‘)) + d(f(x_n‘), g(y’)) < ε. ♦

Properties of the Completion

With the universal property, there’re a couple of properties we can prove rather easily.

Proposition 3. The completion is unique up to homeomorphism, i.e. if $X\hookrightarrow Y$ and $X\hookrightarrow Y'$ are both completions, then there is a unique homeomorphism f : Y → Y’ which restricts to the identity map on X.

Proof.

Let $i:X\to Y$ and $j:X\to Y'$ be the injections. Since i and j are uniformly continuous, by the universal property (U.P.) on Y, there exists a unique uniformly continuous $f:Y\to Y'$ which extends the identity map id_X on X. Likewise, by the U.P. on Y’, there is a unique uniformly continuous $g:Y'\to Y'$ extending id_X. Composing gives uniformly continuous maps $g\circ f:Y\to Y$ and $f\circ g:Y'\to Y'$ extending id_X. By uniqueness in U.P., both $g\circ f$ and $f\circ g$ must be identity maps. ♦

Thus, we can call Y the completion of X without any ambiguity.

If two metrics are topologically equivalent, the resulting completions can be very different. E.g. (0, 1) and R (under the Euclidean metric) are homeomorphic topological spaces, but the former’s completion is [0, 1] while the latter is already complete. In short, completion is not a topological construction.

Proposition 4. If Y is the completion of X and $X'\subseteq X$ , then the completion of X’ is its closure in Y.

Proof.

Let Y’ = cl_Y(X’). Since Y’ is a closed subset of complete metric space Y, it is complete too. Also, X’ is dense in Y’ by definition, so we’re done. ♦

Proposition 5. If Y₁ is the completion of X₁ and Y₂ is the completion of X₂, then Y₁ × Y₂ is the completion of X₁ × X₂, if we let the metric take on any one of the three possibilities in proposition 2.

Proof.

We already know Y₁ × Y₂ is complete by proposition 2. Also, $\text{cl}(X_1\times X_2) = \text{cl}(X_1)\times \text{cl}(X_2) = Y_1\times Y_2$ so X₁ × X₂ is dense in Y₁ × Y₂. ♦

Proposition 6. If Y₁ is the completion of X₁ and Y₂ is the completion of X₂, then any uniformly continuous map $f:X_1\to X_2$ extends to a uniformly continuous $g:Y_1\to Y_2.$

Proof.

Compose f with $X_2\hookrightarrow Y_2$ to obtain a uniformly continuous map $X_1 \to Y_2$ to a complete space. By universal property of Y₂, this extends to a uniformly continuous $g:Y_1\to Y_2$ such that $g|_{X_1} = f.$ ♦

If f is injective or surjective, the induced g may not be so. For example, consider the map $(0, 1)\to \{z\in \mathbf{C} : |z|=1, z\ne 1\}$ which takes t to exp(2πit). We leave it to the reader to prove its uniform continuity. The induced map on the completion is $[0, 1]\to \{z\in\mathbf{C} : |z|=1\}$ which takes t to exp(2πit) as well, and this is not injective.

For another example, consider the map [1, ∞) → (0, 1] which takes x to 1/x. This is uniformly continuous and induces [1, ∞) → [0, 1], again taking x to 1/x. This map is not surjective. Observe that in both examples, the initial map is a homeomorphism but the inverse, though continuous, is not uniformly continuous.

Existence of Completion

Although we’ve proved many properties of the completion of a metric space, we’ve yet to demonstrate its existence.

Big Theorem. Every metric space (X, d) has a completion (Y, d’).

Let’s prove this step-by-step.

Step 1 : Define Y.

Let Σ be the set of all Cauchy sequences in X. Define a relation on Σ:

For $(u_n), (v_n) \in \Sigma,$ write $(u_n) \sim (v_n)$ if $\lim_{n\to\infty} d(u_n, v_n) = 0.$

It’s not hard to prove that this gives an equivalence relation on Σ (the proof’s left as an exercise, e.g. transitivity follows from the triangular inequality). We define Y to be the set of equivalence classes.

Step 2 : Define d’

If two element $y, y'\in Y$ are represented by Cauchy sequences $(u_n), (v_n)\in \Sigma$ we define the distance function to be:

$d'(y, y') := \lim_{n\to\infty} d(u_n, v_n).$

First we show that the limit exists; since R is complete it suffices to show $r_n := d(u_n, v_n)$ is Cauchy. To do that, note that for all m, n:

$\begin{aligned} d(u_n, v_n) &\le d(u_n, u_m) + d(u_m, v_m) + d(v_m, v_n) \\ \implies r_n - r_m &\le d(u_m, u_n) + d(v_m, v_n).\end{aligned}$

By symmetry, we also have $r_m - r_n \le d(u_m, u_n) + d(v_m, v_n)$ which gives:

$|r_m - r_n| \le d(u_m, u_n) + d(v_m, v_n).$

Since $(u_n), (v_n)$ are Cauchy, for any ε>0, we can find N such that whenever m, n > N, we have $d(u_m, u_n), d(v_m, v_n) < \frac\epsilon 2 \implies |r_m - r_n| < \epsilon.$ Thus $(r_n)$ is Cauchy.

Step 3 : Prove that d’ is well-defined.

Let’s show that d’(y, y’) is independent of our choice of Cauchy sequences. Suppose $(u_n) \sim (u_n')$ and $(v_n) \sim (v_n').$ Arguing as in step 2, we obtain:

$|d(u_n', v_n') - d(u_n, v_n)| \le d(u_n, u_n') + d(v_n, v_n').$

By definition of ~, the two terms $d(u_n, u_n')$ and $d(v_n, v_n')$ on the RHS tends to 0. Hence d’ is well-defined.

Step 4 : Prove that d’ is a metric.

Clearly d’(y, y’) ≥ 0. Suppose d’(y, y’) = 0, and $y, y'\in Y$ are represented by $(u_n), (v_n)\in\Sigma.$ Then $\lim_{n\to\infty} d(u_n, v_n) = 0$ , so $(u_n) \sim (v_n)$ and y = y’. This proves reflexivity. Obviously d’(y, y’) = d’(y’, y).

This leaves the triangular inequality. Suppose $(u_n), (v_n), (w_n)\in\Sigma.$ Then we have $d(u_n, w_n) \le d(u_n, v_n) + d(v_n, w_n)$ for each n. Taking the limit of each term, we get the triangular inequality for d’.

Step 5 : Define an embedding of X as a metric subspace of Y.

Define the map i : X → Y which takes x to the element of Y representing the Cauchy sequence (x, x, x, … ). Clearly d’(i(x), i(x’)) = d(x, x’).

Step 6 : Prove that X is dense in Y.

Let $y\in Y$ be represented by $(x_n)\in\Sigma.$ We claim that (x_n), as a sequence in Y, converges to y; i.e. $\lim_{n\to\infty} d'(x_n, y) = 0.$

For each ε>0, pick N such that when m, n > N, we have $d(x_n, x_m) < \frac\epsilon 2.$ Fixing n, and taking the limit as m→∞, we get $d(x_n, y) \le \frac\epsilon 2 < \epsilon.$ Thus, we’re done.

Step 7 : Prove that Y is complete.

Let $(y_n)$ be a Cauchy sequence in Y. Since X is dense in Y, for each n, pick $x_n \in X$ such that $d'(x_n, y_n) < \frac 1 n.$ We claim that $(x_n)$ is Cauchy: for

$d'(x_n, x_m) \le d'(x_n, y_n) + d'(y_n, y_m) + d'(y_m, x_m) < \frac 1 n + \frac 1 m + d'(y_m, y_n).$

Hence for any ε>0, just pick N such that (i) N > 3/ε and (ii) for any m, n > N, we get $d'(y_m, y_n) < \frac\epsilon 3.$ Thus, when m, n > N, we have $d'(x_m, x_n) < \epsilon$ and $(x_n)$ is a Cauchy sequence in X, which must correspond to some $y\in Y.$

It remains to show $(y_n)\to y.$ Indeed, we have:

$d'(y_n, y) \le d'(y_n, x_n) + d'(x_n, y) < \frac 1 n + d'(x_n, y).$

Step 6 then tells us that $d'(x_n, y)\to 0$ since $(x_n) \to y.$ And we’re done. ♦

11 Responses to Topology: Complete Metric Spaces

Conan says:

April 19, 2015 at 2:06 pm

Thanks for the article – I just have a few questions regarding the universal property of completion. Firstly, we have that if f was uniformly continuous, then g is uniformly continuous. If f was a homeomorphism – would this also mean g is a homeomorphism? How would we go about proving this? Lastly, in your proof of g being uniformly continuous, why do you have d'(y,y’)? Isn’t y and y’ elements of Y? To show g is uniformly continuous, don’t we need to show that for d(y,y’) < delta, then d'(g(y),g(y')) < epsilon?

Thanks for any feedback you can provide.

limsup says:

April 19, 2015 at 3:51 pm

For your first question, I believe the answer is yes, but for a rather trivial reason. The resulting X must be complete, so the completion Y is X. In other words, we’re given $f:X\to Z$ such that

(i) f is Cauchy-continuous;
(ii) f is a homeomorphism
(iii) Z is complete.

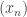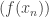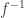Now if $(x_n)$ is Cauchy, then so is $(f(x_n))$ by (i), and this converges to some $z\in Z.$ By (iii), we have z=f(x) for some $x\in X.$ Since $f(x_n) \to f(x)$ and $f^{-1}$ is continuous by (ii), we have $x_n \to x$ .

For your second question, that was a bug, which I’ve now fixed. Thanks! 🙂

- Conan says:
  
  April 19, 2015 at 11:10 pm
  
  Regarding the first part, I’m a bit confused, if you wouldn’t mind explaining. For example, if we had the situation in Proposition 6 above: If $f$ is uniformly continuous, then we can construct a uniformly continuous map $X_{1} \rightarrow Y_{2}$ which would result in a uniformly continuous map in $g$. Suppose $f$ is a homeomorphism between $X_{1}$ and $X_{2}$ – are you saying this must mean that $X_{1}$ and $X_{2}$ are complete? If so – why, I’m struggling to see why this might be the case?
  
  And to follow up with the proof of $g$ being uniformly continuous, I’ve realised I’m still a bit confused when reading through the proof. My understanding is that we need to show that when $d(y,y’) < \delta \implies d'(g(y),g(y')) < \epsilon$, but you seem to have $d(\overline{x_{n}},\overline{x'_{n}}) < \delta \implies d'(g(y),g(y')) < \epsilon$ – could you explain this?
  
  Thanks for your help!
  
  - Conan says:
    
    April 19, 2015 at 11:12 pm
    
    Apologies for the formatting, I thought latex could be used by your reply earlier.
  - limsup says:
    
    April 20, 2015 at 1:01 am
    
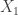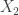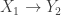    No why must $X_1$ and $X_2$ be complete? If $f:X_1 \to X_2$ is a homeomorphism, then it just extends to a homeomorphism $g:Y_1 \to Y_2$ . The composed map $X_1 \to Y_2$ is not a homeomorphism then. Just take $X_1 = X_2 = \mathbf{Q}$ and $Y_1 = Y_2 = \mathbf{R}$ for instance.
    
    For your second question, I proved that $d(y, y')<\delta/2 \Rightarrow d'(g(y), g(y'))<\epsilon$ .
    
    [ Latex tip for wordpress: use '$' together with latex, e.g. https://en.support.wordpress.com/latex/ ]
Conan says:

April 19, 2015 at 11:22 pm

Sorry, I think I need to clarify my above comment what I am trying to ask is – if f is a homeomorphism – does this mean than g would be a homeomorphism? Thanks.

- limsup says:
  
  April 20, 2015 at 1:06 am
  
  I understood your question and answered it: in my comment I proved that under your assumptions, X has to be complete. Since X is complete, we have Y=X and so if f is a homeomorphism, so is g because g=f.
  
  - Conan says:
    
    April 20, 2015 at 6:44 am
    
    Thanks for the help on the latex.
    
    So to clarify my understanding, what you’re saying is:
    
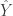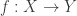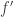    If $\hat{X}$ and $\hat{Y}$ are the completions of $X$ and $Y$ respectively, then if $f:X \rightarrow Y$ is a homeomorphism, then $g$ is a homeomorphism. But the composed map say $f':X \rightarrow \hat{Y}$ is not a homeomorphism. (I suppose because then $f'$ is not surjective – but the image of 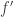$f'$ would be a homeomorphism right?)
    
    How could we prove that the homeomorphism of $f$ just extends to $g$?
    
    Thanks for your patience.
limsup says:

April 21, 2015 at 1:20 am

Oops, I made a mistake in the reply timed (April 20, 2015 at 1:01 am). It’s not true that if f is a homeomorphism, so is g. In fact, I had explicitly listed some counterexamples above after proposition 6. >_<

- Conan says:
  
  April 21, 2015 at 11:47 am
  
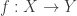  Hi, in your examples above proposition 6, it seems to say that if $f$ is a homeomorphism, then this does not necessarily mean that $g$ is uniformly continuous. But strictly speaking, homeomorphism doesn’t require uniform continuous does it? It just requires a bijective continuous function, with inverse continuous as well right? If $f: X \rightarrow Y$ is a homeomorphism and uniformly continuous, wouldn’t that mean $g$ is also a homeomorphism? With $g$ extending $f':X \rightarrow \hat{Y}$ where $\hat{Y} is the completion of$ latex Y$? In this case, wouldn’t $g$ be uniformly continuous, and it would also be bijective?
  
Bastián says:

May 20, 2021 at 10:36 am

One can, and should prove that the completion is unique up to isometries. The reason why one “should” is that homeomorphisms don’t preserve completeness, so it’s meaningless to consider this property “up to homeomorphism”. Take for instance $\arctan: \mathbb R \to (-\pi/2,\pi/2)$: it’s bijective, continuous and strictly increasing, thus a homeomorphism, and yet the reals are complete while the open interval is not.