We have already seen two forms of unique factorization.
- In a UFD, every non-zero element is a unique product of irreducible (also prime) elements.
- In a Dedekind domain, every non-zero ideal is a unique product of maximal ideals.
Here, we will introduce yet another type of factorization, called primary decomposition. The main idea is that in a noetherian ring, every ideal (even the zero ideal) is an intersection of primary ideals. E.g. in , every non-zero ideal is an intersection of
, ideals generated by prime powers.
Annihilators
Let A be a fixed ring and M be an A-module.
Definition.
The annihilator of
in A is
,
an ideal of A. Similarly, the annihilator of M in A is
,
also an ideal of A. If
, we say M is a faithful A-module.
Note that if , then M can be regarded as a faithful
-module.
Exercise A
1. Given A-submodules , let
.
State and prove the analogue of proposition 2 here for submodules of M. Observe that we can write the annihilators as
Conversely, express in terms of annihilators.
2. Prove that if P is a finitely generated submodule of M.
In particular if M is finitely generated then
.

Support of a Module
Definition.
The support of an A-module M is:
Geometrically, these are points in Spec A at which the module does not vanish.
Proposition 1.
If M is a finitely generated A-module, then
In particular, the support of M is a closed subspace of
.
Proof
Let . For
we have
is zero if and only if there exists
such that
, equivalently if there exists
. Hence
if and only if
.
In the general case, let generate M as an A-module. Then
For the last equivalence, recall that contains
if and only if it contains either
or
. ♦
Proposition 2.
If
is a short exact sequence of A-modules, then
.
If N, P are finitely generated A-modules, then
.
Note
Philosophically, if we imagine the first case as N + P and the second case as N × P, then the result says if and only if both terms are zero whereas
if and only if at least one term is zero.
Proof
Let be prime.
For the first claim, we have a short exact sequence and it follows that
if and only if
.
For the second claim, we have
If or
, clearly the RHS is zero. Conversely if both are non-zero, since they are finitely generated
-modules, Nakayama’s lemma gives
and
. But these are vector spaces over
so we have
♦
Exercise B
1. Let be a homomorphism of finitely generated A-modules; prove that
is a closed subset of Spec A.
2. Prove: if is multiplicative then

Associated Primes
Definition.
Let
be a prime ideal. We say
is associated to the A-module M if
for some
.
Let
be the set of prime ideals of A associated to M.
Note
We have: if and only if there is an injective A-linear map
. Observe that if the annihilator of
is
, then so is that of any non-zero multiple of m; this follows immediately from the definition of prime ideals.
Next suppose M is an -module; we can compute both
and
. There is a bijection
.
In particular, we can compute by considering
as an A-module or a module over itself. The above shows that there is effectively no difference.
Proposition 3.
Suppose A is noetherian. The union of all associated primes of M is its set of zero-divisors
.
In particular, any non-zero A-module M has an associated prime.
Proof
Fix an and
such that
; we need to show a is contained in an associated prime of M.
So let be the set of ideals of A containing a of the form
for
. Since A is noetherian and
, there is a maximal
. We will show
is prime; first write
for some
.
Pick such that
and
. Since
, we have
. And since
, by maximality of
we have
so since
we have
. ♦
Henceforth, A denotes a noetherian ring. However, we do not assume all modules are finitely generated at first.

Properties of Associated Primes
Proposition 4.
Let
be a short exact sequence of A-modules. Then
Proof
We may assume is a submodule and
. The first containment in the claim is obvious. For the second, suppose we have an A-linear map
.
If , then any non-zero
has annihilator
so
. If
, then composing
is still injective, so
. ♦
Corollary 1.
We have
.
Proof
Follows immediately from proposition 4. ♦
Next, we show that taking the set of associated primes commutes with localization.
Proposition 5.
Let
be a multiplicative subset. Then
Proof
(⊇) If and
, then localization at S gives an A-linear map
.
(⊆) Suppose we have an -linear map
where
is prime. By theorem 1 here, we can write
for some prime
such that
. Now in the injection
we let
be the image of 1. It remains to show: there exists
such that
.
For each , we have
in
so that
in M for some
, i.e.
. Pick a generating set
of
; then for each i there exists
with
. Then
satisfies
.
Conversely if then
so
lies in the annihilator of
, i.e. in
. Then
; since
we have
. ♦


How to conclude that in the last line in proposition 2?
in the last line in proposition 2?
Recall that thus the module
thus the module  is obtained by quotienting the former module (i.e. by tensoring with
is obtained by quotienting the former module (i.e. by tensoring with 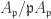 ). So if the latter is non-zero so is the former.
). So if the latter is non-zero so is the former.
In statement of proposition 3 , it is mentioned in the end that a y nonzero module has an associated prime. It may happen that M is a faithful A module and A need not be a integral domain. Am i missing something obvious?
In your example, the associated prime would be 0. Thus we get an injection .
.