“Every mathematician knows it is impossible to understand an elementary course in thermodynamics.” – V. I. Arnold.
The following is the culmination of at least three attempts to understand thermodynamics at various times during the last two years. Why’s it so hard, you might wonder? In hindsight, I’m not entirely sure either, but I do know that thermodynamics has broken the record for my number of iterations of the confusion-clarification cycle which one must inevitably encounter when learning a new topic.
You might also wonder why there’s a post about physics in this blog. Not only is this non-Olympiad, but it doesn’t even appear related to mathematics. However, classical thermodynamics is based on a deductive system which is particularly appealing and satisfying to a mathematician’s sensibilities. One can think of the four (not three!) laws of thermodynamics as the axioms, and obtain the theory via a mixture of deductions and physical intuition. The level of rigour of course is not as airtight as that of a mathematical theory, but coupled with some basic physical assumptions it should suffice.
Finally, I must confess I’m a bit jittery about writing a post on physics here, since there will no doubt be errors in the post. For this, I beg the readers to be patient and any corrections will be appreciated. If you wish a proper treatment of thermodynamics which is similar in spirit to what I have here, there are:
- Enrico Fermi, “Thermodynamics“, Dover Publications, 1936.
- A. B. Pippard, “The Elements of Classical Thermodynamics“, Cambridge University Press, 1966.
1. Basic Concepts
Ok let’s begin with the definitions. To fix ideas, we will assume that our system comprises of one or more types of liquids/gases. The system is said to be in equilibrium if there is no discernible macroscopic change over time, although on a microscopic level things are certainly far from tranquil. We will assume all systems to be in equilibrium unless otherwise stated. When a system is in equilibrium, we can then define the state of the system by a list of values, known as state variables, which can be measured.
Example 1. If the system comprises of a single homogeneous gas, then we may measure the volume (V), the pressure (P) and the number of particles (N). These are the only variables we consider for now. What about the temperature, you might ask? Problem is, we don’t know how to define the temperature. Indeed, both volume and pressure make sense from the theory of classical mechanics, but not temperature. In fact, part of the purpose of thermodynamics is to introduce, define and develop the concept of temperature.
Example 2. If the system comprises of two gases separated by a wall, then we need to provide the parameters for each gas, i.e. and
.
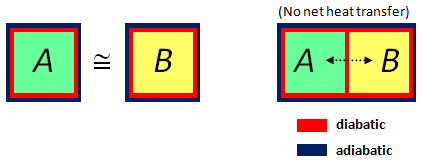
Now, a stand-alone system may exchange energy with the environment in the form of heat. A system is said to be adiabatically sealed if no such exchange takes place. A wall separating two systems is said to be diabatic if heat exchange can take place – however, the presence of the wall means material exchange does not occur. In short: diabatic = possible heat exchange; adiabatic = no heat exchange. In both cases, particles don’t cross the wall.
The next definition is extremely important.
Given two systems, we say they are in thermal equilibrium (T.E.) if, when we separate them by a diabatic wall (and seal the whole union adiabatically), no net exchange of heat takes place.
Clearly, the concept of T.E. satisfies the following:
- reflexive (every system is in T.E. with itself, by sheer definition);
- symmetric (if system A is in T.E. with system B, then so does system B with system A).
The Zero-th Law of Thermodynamics then states that T.E. is transitive, which means it is an equivalence relation!
Zero-th Law of Thermodynamics. If system A is in T.E. with system B, and system B is in T.E. with system C, then system A is in T.E. with system C.
Now we’re ready to define temperature. We shall define the abstract temperature to be the equivalence class of all systems, under thermal equilibrium. [ For those who don’t know equivalence classes, we take all systems at T.E. with each other and assign a unique label to each one, calling it its temperature. ] Unfortunately, that’s an abstract definition, and we can’t make head or tail out of it in practice, let alone perform computations.
Example 3. Consider two separate homogeneous gases, parametrised by (P, V, N) and (P’, V’, N’) as in example 1 above (adiabatically sealed of course). If we bring them together, there will be a real-valued function f(P, V, N) such that the two gases are in T.E. if and only if:
f(P, V, N) = f(P’, V’, N’).
In the case of an ideal gas, kinetic theory of gases (which we shan’t go into here) gives us Boyle’s law, so we can take f(P, V, N) = PV/N. A more realistic model, however, is the van der Waal’s equation , where v = V/N. Notice that the ideal gas equation is the limiting case of van der Waal’s equation where a = b = 0. [ Van der Waal’s equation assumes that particles have positive size and have mutually attractice / repulsive forces, hence the difference. But we digress. ]
Anyway, in the case of an ideal gas, we could take the temperature to be PV/N. But let’s not do that, since it requires us to peg the temperature to a fixed type of system which does not even exist in reality, namely that of a homogeneous ideal gas.
2. When the State Changes
A system may not remain at the same state forever. Hence, we will look at processes whereby a system may change its state from A to B (e.g. when a gas is compressed). At each time step during the process, we may take instant snapshots and consider the state of the system. This forms a curve in a multi-dimensional space, where the number of dimensions is precisely the number of state variables.
But there’s a problem: notice we only defined states for systems at equilibrium, whereas if a system changes its state too quickly, the snapshots may not be at equilibrium. Hence, we will assume the ideal case of quasi-static processes, i.e. processes which occur so slowly that the instant snapshots that we take are always in equilibrium. From now onwards, we will assume all processes are quasi-static unless otherwise stated. Thus it makes sense to talk about the path of the system in the state space.
Example 4. In the case of a homogeneous gas sealed within an elastic chamber, the number of particles N remains unchanged, so a quasi-static process is given by a path on the P–V plane.
The next definition is key to the whole theory of thermodynamics.
A process is said to be a reversible cycle if the states of the entire universe at the initial and final points are identical. More generally, a process is said to be reversible if it is part of a reversible cycle.
 Important! A reversible process always has to be considered from a global scale. Later on, we will talk about a certain system undergoing a reversible process. By that, we mean that it is possible to reverse the entire process on a global scale, i.e. it is possible to bring the whole universe back to the initial state. In particular, if we have a homogeneous gas and we only look at the path on the P–V plane, we cannot tell if the process is reversible without knowing what the exact process is!
Important! A reversible process always has to be considered from a global scale. Later on, we will talk about a certain system undergoing a reversible process. By that, we mean that it is possible to reverse the entire process on a global scale, i.e. it is possible to bring the whole universe back to the initial state. In particular, if we have a homogeneous gas and we only look at the path on the P–V plane, we cannot tell if the process is reversible without knowing what the exact process is!
We repeat: reversible processes must be global.
Or, instead of looking at the whole universe, we could just seal a system adiabatically and look at it in isolation. Since we’re only looking at heat transfer, this cuts off all interactions between a system and its environment; specifically, we could imagine the process taking place inside the system while the rest of the universe stands still. It wouldn’t make an iota of difference to the system anyway because it’s adiabatically sealed from it.
Of course, if all processes are reversible, this definition would be vacuous. The whole point of the Second Law of Thermodynamics is that this is not true. One usually speaks of two variants – Clausius Law and Kelvin Law – but to make sense of Clausius Law, one needs to consider the work done by the system. And for that, one requires the First Law….
(To be continued…)




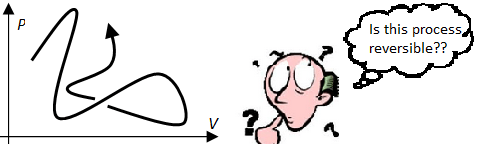
This is a really nice post! Note a small typo: In the paragraph beginning, “Now we’re ready to define,” I think you mean to say not “equilibrium classes” but “equivalence classes.” Just didn’t want this small issue to mar an otherwise great exposition.
Thanks for the correction! Glad you liked the articles. 🙂
Oh my goodness! This post is amazing! I’m a math student, and I’m self-studying classical thermodynamics. I’ve never really studied physics before, and it is surprising how different the cultures are. It’s difficult for me to understand the text I’m reading. Or maybe thermodynamics is just confusing?
Anyway, what really got me excited about your post was specifically the thermal equilibrium being an equivalence relation and temperature as the equivalence classes. That makes it so clear! So obvious! Thank you for saying so. And for saying the definition doesn’t help in practice. (Because as a reader/student, I already know about thermometers…)
Thermodynamics is confusing! I am a mathematics and physics student and thermodynamics is a wild deviation from the content I’m used to learning. This is because thermodynamics, at least at this introductory level, is a descriptive science opposed to more “usual” physics which is deductive, such as classical mechanics, electromagnetic theory, and quantum mechanics. Often there is a mathematical basis which you build the physics out of, rather than starting with behavior and building math from that. This is very challenging, but I think an important perspective to have.
Two basic points.
1. What is (equilibrium) thermodynamic state? An operational definition is needed.
2. The notion of “quasi-static” process is empty: any adiabatic change is irreversible. Caratheodory admitted it.
Thermodynamics must be formulated based on operational definitions in terms of measurable quantities.
How does one define heat, exactly? Also, does the definition for reversible process imply that $(P_1,V_1,N_1) = (P_2,V_2,N_2)$? I loved this post, though. My issue, when I took thermodynamics in undergradute and graduate school (mayhaps this is an error on my part), is that I never quite understood how things were defined, but this post actually makes sense to me, so thank you.
I’m afraid heat (i.e. energy) is a fundamental physical variable which can’t really be defined; at least I can’t. Rather one postulates the existence of such a scalar quantity. In statistical mechanics, the energy is the sum of the kinetic energy of individual atoms, but this further assumes that matter is comprised of atoms. Thermodynamics makes no such assumptions.
For a reversible process of an ideal gas, think of (P(t), V(t), N(t)) as a triple which varies according to time t. Each variable doesn’t have to be constant. But in thermodynamics, we don’t even need to assume the existence of (P, V, N) in the system. Notice that this triple only appears as an example, to help illustrate the theory.