We have already seen symmetric polynomials and some of their applications in an earlier article. Let us delve into this a little more deeply. Consider the ring of integer polynomials. The symmetric group
acts on it by permuting the variables; specifically,
takes:
For example, takes
to
. Denote the ring of symmetric polynomials by:
This is a homogeneous ring, written as a direct sum:
where is the additive group of homogeneous polynomials of degree
. For example, when
, we have (upon renaming the variables to x, y, z):
Let us fix n, the number of variables.

Monomial Basis
Clearly, each is a free additive abelian group. For example, for
, a basis is given by:
More generally, recall that a partition of
is a sequence of non-negative integers:
Two partitions of are considered the same if we can obtain one from the other by appending or dropping zeros. E.g. (3, 2, 1, 0) and (3, 2, 1) are identical partitions of 6.
Definition. Given a partition
of
, let
be the symmetric polynomial obtained by summing all terms of the form:
For example when
, we have
, and
.
The following result is clear.
Theorem. The additive group
is free with basis given by
, for all partitions
of
into at most
parts.
Let us consider an example where . A basis of
is given by:
Note that for brevity of notation, we write instead of
. However, if the subscripts involve variables, we will include the commas for clarity.

Elementary Symmetric Polynomials
Recall that the elementary symmetric polynomials in x, y, z are given by x+y+z, xy+yz+zx and xyz. Generalizing this, we define:
Furthermore, given a partition of
, we define:
assuming . Note that since
, we can take as many terms as we want by increasing
without affecting
For example, when
we have:
Now since (here,
where
denotes the sum of all
), it is natural to ask the following question.
Task. Express the symmetric polynomial
as a
-linear combination of the monomial polynomials
for various
In our above example, expanding with WolframAlpha gives us:
In the remaining of this article, we will describe a more systematic method of computation.

Expanding the e‘s
Here is our main result.
Theorem. Suppose
. Consider the expression
where we sum over all partitions
with
The coefficient
is given by the number of matrices
with entries either 0 or 1 such that
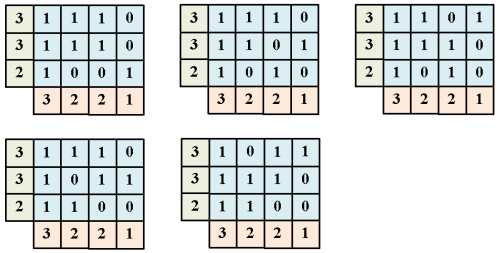
Here is a sample computation: take the polynomial above and find the coefficient for the monomial
For that, we need to find the number of binary matrices with column sums
and row sum
As expected, we get 5 solutions:
Proof of Theorem.
Using the above example with , we expand
and attempt to find the coefficient of
E.g. suppose
and
We wish to expand:
Here is one way we can multiply terms to obtain
Thus each binary matrix corresponds to a way of obtaining by multiplying terms from
,
, etc. ♦
 In the definition of
In the definition of , the variable n is ostensibly missing. However note that if
, then the monomial
since it would involve more than n variables. For example, if
and
, then the above expansion gives
since
One can verify this directly by expanding
On the other hand, if , we now have
and now

Exercise
1. Express as a linear combination of the monomial symmetric polynomials:
Check your computations with WolframAlpha.
2. Write a program in Python (or any language) which computes for any partitions

I think in the last theorem there should be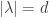
Thanks. Corrected.
Can you give your mail. My mail id m——-@gmail.com.
[ Author: thanks. I’ve edited your email to prevent people from spamming you. ]
Please reply. Actually i don’t know your mail.. thank you.