Basic Definitions
The objective of this article is to establish the theory of transcendence bases for field extensions. Readers who are already familiar with this may skip the article. We will focus on field extensions here.
Definition.
Let
be a field extension. Elements
are said to be algebraically dependent over K if
Otherwise,
are algebraically independent over K.
We say
forms a transcendence basis of L over K if it is algebraically independent over K and L is algebraic over
.
If such a basis exists for
, we say L has finite transcendence degree over K, and write
,
the transcendence degree of L over K.
Exercise A
Prove that if then
so
forms a transcendentce basis of L over
.
Note that a priori, it is not clear that the transcendence basis is well-defined: could we perhaps choose two transcendence bases of different sizes? The answer is no as we will see.
Lemma 1.
For
write
for the field extension of K generated by
.
If
are algebraically independent over K, then every element of L’ can be uniquely written as
as
runs through all rational functions
. Thus we have an isomorphism:
.
Proof
Consider the K-algebra homomorphism which takes
for each
. By definition of algebraic independence this map is injective so we get an embedding
of fields, whose image is clearly L’. ♦

Swapping Lemma
The following will be repeatedly used throughout the article.
Key Observation.
Let
be a field extension and
be algebraically independent over K. Let
.
Then
are algebraically dependent over K if and only if
is algebraic over
.
Note
Compare this with the linear algebra variant: if V is a vector space and are linearly independent, then for
,
are linearly dependent if and only if w is a linear combination of
.
Proof
(⇒) If are algebraically dependent over K we have a non-zero polynomial
such that
. This polynomial must involve Y or we would obtain a polynomial relation in
, a contradiction. Taking
,
we see that and
. ♦
(⇐) If is algebraic over
pick
, not all zero, such that
Clearing denominators, we assume each so
for some non-zero polynomial
with coefficients in K. ♦
Here is the main result.
Swapping Lemma.
Let
be a transcendence basis of L over K and
be transcendental (i.e. not algebraic) over K. Then there exists an
such that
form a transcendence basis of L over K.
Furthermore if
are algebraically independent over K, then we can pick
from
.
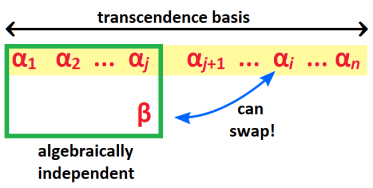
Proof
By assumption is algebraic over
. Thus by the key observation,
are algebraically dependent. Assume
are algebraically independent but
are algebraically dependent.
We claim that swapping with
also gives a transcendence basis.
Indeed let . By the key observation,
is algebraic over
and hence over K’. So we have algebraic extensions
.
It remains to show that are algebraically independent. If not, by the key observation
is algebraic over
and we have algebraic extensions
, so
is algebraic over
, a contradiction. ♦

Transcendence Degree is Well-Defined
Proposition 1.
If
is a transcendence basis for
and
are algebraically independent over K, then
and
- we can replace m terms of
by
to obtain another transcendence basis for L over K.
Proof
We repeatedly apply swapping lemma. If m = 0, there is nothing to prove; otherwise by swapping lemma, we can swap out some element of with
to obtain another transcendence basis.
At each stage, suppose we have a transcendence basis together with n–j elements of
. If j = m we are done. If j = n then
is already a transcendence basis so we also have j = m. Hence suppose
and
.
Since are algebraically independent, swapping lemma asserts we can swap out another
with
so we get a transcendence basis
together with n–j-1 elements of
. Eventually, we obtain a transcendence basis comprising of
with n – m elements of
. ♦
Corollary 1.
Any two transcendence bases of L/K have cardinality n so
is well-defined.
Proof
For any transcendence bases and
, proposition 1 says
and
. ♦

Transitivity
Lemma 2.
Let
be a field extension and
such that L is algebraic over
.
Then
contains a transcendence basis of L over K.
Proof
Pick a maximal algebraically independent subset of . Upon reordering suppose this is
; set
. By maximality of
, each of
is algebraic over
. Hence we get algebraic extensions
and we are done. ♦
Proposition 2.
Let
be field extensions. Then M has finite transcendence degree over K if and only if M has finite transcendence degree over L and L has finite transcendence degree over K, in which case
Proof
(⇒) Let be a transcendence basis of M over K. In particular M is algebraic over
so by lemma 2, there exists a subset of
which forms a transcendence basis of M over L.
Next suppose are algebraically independent over K. By proposition 1,
so there exists a maximal algebraically independent sequence
for L/K. By key observation it follows that any
is algebraic over
.
(⇐) Pick transcendence bases for L over K, and
for M over L. We claim that
form a transcendence basis of M over K, which would complete the proof.
Suppose for a non-zero
. Then
is a polynomial relation for
; since these are algebraically independent we have
. But the coefficients of q are polynomials in
; since
are algebraically independent, we also get
.
Finally, since is algebraic, so is
since the RHS is generated as a field by L and , all algebraic over the LHS. Furthermore,
is algebraic by assumption. Thus
is an algebraic extension as desired. ♦
Exercise B
Let where
is irreducible. Prove that
has transcendence degree n – 1 over K.


Can you please check the proof of Proposition . Especially the statement. “… Hence suppose j>n and j>m….” Also in the preceding statement how does it follow that
. Especially the statement. “… Hence suppose j>n and j>m….” Also in the preceding statement how does it follow that 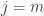 ?
?
You’re right it should be j < n and j < m.
Next on your question why j = m. If j < m, then is a transcendence basis so L is algebraic over
is a transcendence basis so L is algebraic over  so
so  is algebraic over
is algebraic over  which is a contradiction.
which is a contradiction.